网址：http://m.1010jiajiao.com/timu_id_4439781[举报]
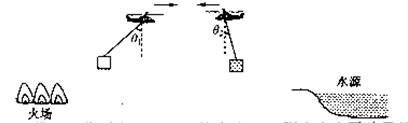
（07江苏）（14分）直升机沿水平方向匀速飞往水源取水灭火，悬挂着m＝500 kg空箱的悬索与竖直方向的夹角θ1＝45°。直升机取水后飞往火场，加速度沿水平方向，大小稳定在a＝1.5 m/s2时，悬索与竖直方向的夹角θ2＝14°。如果空气阻力大小不变，且忽略悬索的质量，试求水箱中水的质量M。
（取重力加速度g＝10 m/s2；sin14°＝0.242；cos14°＝0.970）
07江苏 28 （13分）如（a）图，质量为M的滑块A放在气垫导轨B上，C为位移传感器，它能将滑块A到传感器C的距离数据实时传送到计算机上，经计算机处理后在屏幕上显示滑块A的位移－时间（s－t）图象和速率－时间（v－t）图象。整个装置置于高度可调节的斜面上，斜面的长度为l、高度为h。（取重力加速度g＝9.8 m/s2，结果可保留一位有效数字）
⑴现给滑块A一沿气垫导轨向上的初速度，A的v－t图线如（b）图所示。从图线可得滑块A下滑时的加速度a＝ m/s2 ,摩擦力对滑块A运动的影响 。（填“明显，不可忽略”或“不明显，可忽略”）
⑵此装置还可用来验证牛顿第二定律。实验时通过改变 ，可验证质量一定时，加速度与力成正比的关系；实验时通过改变 ，可验证力一定时，加速度与质量成反比的关系。
⑶将气垫导轨换成滑板，滑块A换成滑块A/，给滑块A/一沿滑板向上的初速度，A/的
s－t图线如（c）图。图线不对称是由于 造成的，通过图线可求得滑板的倾角θ＝ （用反三角函数表示），滑块与滑板间的动摩擦因数μ＝
查看习题详情和答案>>
07江苏 18 、（14分）如图所示，巡查员站立于一空的贮液池边，检查池角处出液口的安全情况。已知池宽为L，照明灯到池底的距离为H。若保持照明光束方向不变，向贮液池中注入某种液体，当液面高为
时，池底的光斑距离出液口
。
⑴试求当液面高为
时，池底的光斑到出液口的距离x。
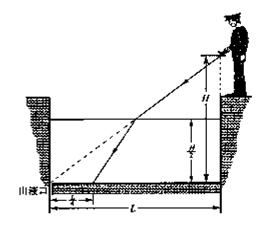⑵控制出液口缓慢地排出液体，使液面以v0的速率匀速下降，试求池底的光斑移动的速率vx。
07江苏 21（16分）如图所示，空间等间距分布着水平方向的条形匀强磁场，竖直方向磁场区域足够长，磁感应强度B＝1 T，每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d＝0.5 m，现有一边长l＝0.2 m、质量m＝0.1 kg、电阻R＝0.1 Ω的正方形线框MNOP以v0＝7 m/s的初速从左侧磁场边缘水平进入磁场，求：
⑴线框MN边刚进入磁场时受到安培力的大小F；
⑵线框从开始进入磁场到竖直下落的过程中产生的焦耳热Q；
⑶线框能穿过的完整条形磁场区域的个数n。
查看习题详情和答案>>07江苏
60（9分）要描绘某电学元件（最大电流不超过6 mA，最大电压不超过7 V）的伏安特性曲线，设计电路如图，图中定值电阻R为1 kΩ，用于限流；电流表量程为10 mＡ，内阻约为5 Ω；电压表（未画出）量程为10 Ｖ，内阻约为10 kΩ；电源电动势E为12 Ｖ，内阻不计。
⑴实验时有两个滑动变阻器可供选择：
a、阻值0到200 Ω，额定电流0.3 A
b、阻值０到20 Ω，额定电流0.5 A
本实验应选的滑动变阻器是 （填“a”或“b”）
⑵正确接线后，测得数据如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| U（V） | ０.00 | 3.00 | 6.00 | 6.16 | 6.28 | 6.32 | 6.36 | 6.38 | 6.39 | 6.40 |
| I（mA） | 0.00 | 0.00 | 0.00 | 0.06 | 0.50 | 1.00 | 2.00 | 3.00 | 4.00 | 5.50 |
a）根据以上数据，电压表是并联在M与
之间的（填“O”或“P”）
b）根据以上数据，画出该元件的伏安特性
曲线为 。
⑶画出待测元件两端电压UMO随MN间电压UMN变化的示意图为（无需数值）
 |
