摘要： 如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B.右端连在固定板上.放在光滑绝缘的水平面上.整个装置处在场强大小为E.方向水平向右的匀强电场中.现有一质量为m.带电荷量为+q的小球A.从距B球为S处自由释放.并与B球发生碰撞.碰撞中无机械能损失.且A球的电荷量始终不变.已知B球的质量M=3m.B球被碰后作周期性运动.其运动周期. (1)求A球与B球第一次碰撞后瞬间.A球的速度V1和B球的速度V2, (2)要使A球与B球第二次仍在B球的初始位置迎面相碰.求劲度系数k的可能取值. 答案 :(1)设A球与B球碰撞前瞬间的速度为v0. 由动能定理得. ① 解得: ② 碰撞过程中动量守恒 ③ 机械能无损失.有 ④ 解得 负号表示方向向左 方向向右 (2)要使m与M第二次迎面碰撞仍发生在原位置.则必有A球重新回到O处所用的时间t恰好等于B球的 ⑥ (n=0 .1 .2 .3 --) ⑦ 由题意得: ⑧ 解得: (n=0 .1 .2 .3 --) ⑨
网址：http://m.1010jiajiao.com/timu_id_4438048[举报]
（2009?茂名二模）矩形导线框abcd放在匀强磁场中，在外力控制下静止不动，磁感线方向与线圈平面垂直，磁感应强度B随时间变化的图象如图甲所示．t=0时刻，磁感应强度的方向垂直纸面向里；在0～4s时间内，线框ab边受匀强磁场的作用力随时间变化的图象（力的方向规定以向左为正方向）是图中的（ ）
查看习题详情和答案>>
（2009?茂名一模）如图所示，光滑水平轨道与光滑圆弧轨道相切，轻弹簧的一端固定在轨道的左端，OP是可绕O点转动的轻杆，且摆到某处就能停在该处；另有一小钢球．现在利用这些器材测定弹簧被压缩时的弹性势能．（1）还需要的器材是
天平
天平
、刻度尺
刻度尺
．（2）以上测量实际上是把对弹性势能的测量转化为对
重力势
重力势
能的测量，进而转化为对质量
质量
和上升高度
上升高度
的直接测量． （3）为了研究弹簧的弹性势能与劲度系数和形变量的关系，除以上器材外，还准备了两个轻弹簧，所有弹簧的劲度系数均不相同．试设计记录数据的表格．
（2009?茂名二模）如图所示，位于竖直平面内的坐标系xoy，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B，还有沿x轴负方向的匀强电场，场强大小为E．在其第一象限空间有沿y轴负方向的、场强为E′=| 4 | 3 |
（1）油滴的电性；
（2）油滴在P点得到的初速度大小；
（3）油滴在第一象限运动的时间和离开第一象限处的坐标值．
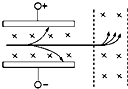（2009?茂名一模）如图所示，一束质量、速度和电荷量不同的正离子垂直地射入匀强磁场和 匀强电场正交的区域里，结果发现有些离子保持原来的运动方向，有些未发生任何偏转．如果让这些不偏转的离子进入另一匀强磁场中，发现这些离子又分裂成几束，对这些进入另一磁场的离子，可得出结论（ ）
（2009?茂名一模）如图所示，电路中当可变电阻R的阻值增大时（ ）