摘要：18．(1)∵ 数列{ an }的前n项和为Sn = 2n+1-n-2. ∴ a1 = S1 = 21+1-1-2 = 1． -------- 1分 当n≥2时.有 an = Sn-Sn-1 = (2n+1-n-2)-[ 2n-(n-1)-2 ] = 2n-1． -------- 4分 又 ∵ n = 1时.也满足an = 2n-1. ∴ 数列{ an }的通项公式为 an = 2n-1(n∈N*)． -------- 6分 (2)∵ .x.y∈N*.∴ 1 + x = 1.2.3.6. 于是 x = 0.1.2.5. 而 x∈N*.∴ B = { 1.2.5 }． -------- 9分 ∵ A = { 1.3.7.15.-.2n-1 }.∴ A∩B = { 1 }． -------- 12分
网址：http://m.1010jiajiao.com/timu_id_4437092[举报]
(n∈N*)．
．数列{an}的前n项和为Sn，若a1＝2且Sn＝Sn－1＋2n(n≥2，n∈N*)．
(1)求Sn；
(2)是否存在等比数列{bn}满足b1＝a1，b2＝a3，b3＝a9？若存在，则求出数列{bn}的通项公式；若不存在，则说明理由．
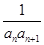}的前n项和为Tn，求证：
≤Tn<
.
| |||||
为等差数列，并求{bn}的通项公式；
}的前n项和为Tn，
求证：
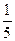≤Tn<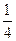
.