摘要:11.(1)已知.求的值. ,且sinθ,cosθ是关于x的方程 5x2-x+m=0的根,求sin3θ+cos3θ和tanθ的值. 解:(1)条件中的表示10条不同终边的角.这10条终边分成5组.每组互为反向延长线.余弦值的和为零. ∴f = f+f =f (2)由韦达定理得: ① 由(sinθ+cosθ)2=1+2sinθcosθ得 ∴, Sin3θ+xos3θ=(sin2θ-sinθcosθ+cos2θ) = = 又0<θ<π,sinθcosθ<0, ∴sinθ>0,cosθ<0 sinθ-cosθ= . [探索题]是否存在α.β.α∈(-.).β∈使等式sin(3π-α)=cos(-β).cos(-α)=-cos(π+β)同时成立?若存在.求出α.β的值,若不存在.请说明理由. 解:由条件得 ①2+②2得sin2α+3cos2α=2.∴cos2α=. ∵α∈(-.).∴α=或α=-. 将α=代入②得cosβ=.又β∈. ∴β=.代入①可知.符合. 将α=-代入②得β=.代入①可知.不符合. 综上可知α=.β=. 备选题: 已知sinα是方程5x2+7x-6=0的根,且,求 的值. 解:解方程5x2+7x-6=0得,x1=-2(舍),x1=. ∴所求式=1+tan2α=
网址:http://m.1010jiajiao.com/timu_id_4434058[举报]
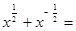 3,求
3,求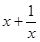 的值;
的值; 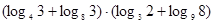
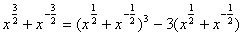 的值;
的值;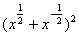 .
. ,求
,求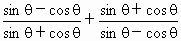 的值.
的值.
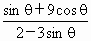 的值.
的值.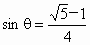 ,求
,求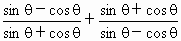 的值.
的值.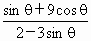 的值.
的值.