摘要:例1.从边长为2a的正方形铁皮的四角各截去一小块边长为x的正方形.再将 四边向上折起.做成一个无盖的方铁盒.问x取何值时.盒的容积最大? 最大的容积为多少? 例2.某杂志若以每本2元的价格出售.可以发行10万本.若每本价格提高0.2元.发行量就少5000本.要使销售总收入不低于22.4万元.则该杂志的定价最高和最低各为多少? 例3.在某海滨城市附近海面有一台风.根据监测.当前台风中心位于城市O的东偏南()方向300km的海面P处.并且以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域.当前半径为60km.并且以10km/h的速度不断增大.问几个小时后.该城市开始受到台风的侵袭? *例4.甲.乙两地相距240千米,汽车从甲地匀速行驶到乙地,速度不得超过60千米/时.已知汽车每小时的运输成本由可变部分和固定部分组成:可变部分与速度v的平方成正比,比例系数为b,固定部分为a元. ⑴全程运输成本把y(元)表示为速度v的函数,并指出这个函数的定义域; ⑵为了使全程运输成本最小,汽车应以多大速度行驶?
网址:http://m.1010jiajiao.com/timu_id_4430133[举报]
如图(1),从边长为2a的正方形铁片的四个角各截一个边长为x的正方形,然后折成一个无盖的长方体盒子,如图(2),要求长方体的高度x与底面正方形边长的比不超过正常数t.
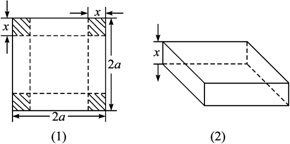
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t.问:
(1)求长方体的容积V关于x的函数表达式;
(2)x取何值时,长方体的容积V有最大值? 查看习题详情和答案>>
(1)求长方体的容积V关于x的函数表达式;
(2)x取何值时,长方体的容积V有最大值? 查看习题详情和答案>>
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t.问:
(1)求长方体的容积V关于x的函数表达式;
(2)x取何值时,长方体的容积V有最大值?
查看习题详情和答案>>
(1)求长方体的容积V关于x的函数表达式;
(2)x取何值时,长方体的容积V有最大值?
查看习题详情和答案>>