摘要:常用正面词语的否定如下表: 正面词语 否定 正面词语 否定 等于 不等于 任意的 某个 小于 不小于 所有的 某些 大于 不大于 至多有一个 至少有两个 是 不是 至少有一个 一个也没有 都是 不都是
网址:http://m.1010jiajiao.com/timu_id_4429342[举报]
(1)一般地,用p和q分别表示原命题的条件和结论,用 和
和 分别表示p和q的否定,于是四种命题的形式就是:?
分别表示p和q的否定,于是四种命题的形式就是:?
原命题:若p则q(p ![]() q);?
q);?
否命题:若 则 ( );?
逆命题:若 则 ( );?
逆否命题:若 则 ( ).?
(2)四种命题的关系?
?
注意:①一个命题和它的逆否命题同真假,而与它的其他三个命题的真假无此规律.?
②要严格区别命题的否定与否命题之间的差别.?
对一个命题进行否定,就要对正面叙述的词语进行否定,而否命题既否定条件又否定结论.例如,原命题“若∠A=∠B,则a=b”的否定形式为“若∠A=∠B,则a≠b”,而其否命题则为“若∠A≠∠B,则a≠b”.?
(3)反证法?
①定义: .?
②使用反证法的条件.?
(ⅰ)直接证困难较大时;?
(ⅱ)当待证命题的结论中出现“不可能”“不是”“至少”“至多”“唯一”等限制性很强的条件时.?
③一般步骤:?
(ⅰ) ;?
(ⅱ) .
查看习题详情和答案>>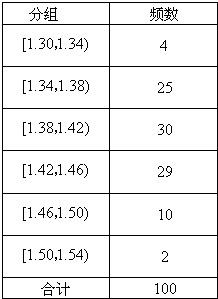 在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:(I)画出该产品纤度的频率分布直方图;
(II)估计纤度落在[1.38,1.50)中的概率及纤度小于1.40的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值(例如区间[1.30,1.34)的中点值是1.32)作为代表.据此,估计纤度的期望. 查看习题详情和答案>>
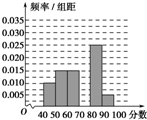 某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,补全这个频率分布直方图后,估计本次考试中的平均分(统计方法中,同一组数据常用该组区间的中点值作为代表)( )
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,补全这个频率分布直方图后,估计本次考试中的平均分(统计方法中,同一组数据常用该组区间的中点值作为代表)( )
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ)测得该年级所抽查的100名同学身高(单位:厘米)频率分布直方图如右图:
(ⅰ)统计方法中,同一组数据常用该组区间的中点值(例如区间[160,170)的中点值为165)作为代表.据此,计算这100名学生身高数据的期望μ及标准差φ(精确到0.1);
(ⅱ)若总体服从正态分布,以样本估计总体,据此,估计该年级身高在(158.6,181.4)范围中的学生的人数.
(Ⅲ)如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
(ⅰ)完成上表;
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K2=
,参考数据:
查看习题详情和答案>>
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ)测得该年级所抽查的100名同学身高(单位:厘米)频率分布直方图如右图:
(ⅰ)统计方法中,同一组数据常用该组区间的中点值(例如区间[160,170)的中点值为165)作为代表.据此,计算这100名学生身高数据的期望μ及标准差φ(精确到0.1);
(ⅱ)若总体服从正态分布,以样本估计总体,据此,估计该年级身高在(158.6,181.4)范围中的学生的人数.
(Ⅲ)如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K2=
| π(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
