摘要： 点O是三角形ABC所在平面内的一点.满足.则点O是的 A. 三个内角的角平分线的交点 B .三条边的垂直平分线的交点 C.三条中线的交点 D. 三条高的交点
网址：http://m.1010jiajiao.com/timu_id_4429238[举报]
（05年全国卷Ⅰ文）点O是三角形ABC所在平面内的一点，满足
，则点O是
的
（A）三个内角的角平分线的交点 （B）三条边的垂直平分线的交点
（C）三条中线的交点 （D）三条高的交点
查看习题详情和答案>>
选修4-1：几何证明选讲如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于B、C两点，∠APC的平分线分别交AB、AC于点D、E．
（I）证明：AD=AE；
（II）已知∠C=30°，求
| PC | PA |
（2012•上饶一模）椭圆C1：
+y2=1(a＞0)与双曲线C2：
-y2=1(m＞0)有公共焦点，左右焦点分别为F1，F2，曲线C1，C2在第一象限交于点P，I是△PF1F2内切圆圆心，O为坐标原点，F2H垂直射线PI于H点，|OH|=
，则I点坐标是
查看习题详情和答案>>
| x2 |
| a2 |
| x2 |
| m2 |
| 2 |
(
，2-
)
| 2 |
| 3 |
(
，2-
)
．| 2 |
| 3 |
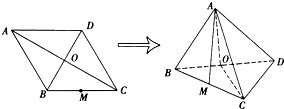已知菱形ABDC的边长为2，对角线AC与BD交于点O，且∠ABC=120°，M为BC的中点．将此菱形沿对角线BD折成直二面角A-BD-C．