摘要：如图.在平面直角坐标系中.矩形OABC的顶点A(0.3).C(.0)．将矩形OABC绕原点顺时针旋转90°.得到矩形．设直线与轴交于点M.与轴交于点N.抛物线的图象经过点C.M.N．解答下列问题: (1)分别求出直线和抛物线所表示的函数解析式, (2)将△MON沿直线MN翻折.点O落在点P处.请你判断点P是否在抛物线上.说明理由． (3)将抛物线进行平移.使它经过点.求此时抛物线的解析式． [命题意图]考查二次函数.图形翻折等综合应用能力.考查思维的深刻性 [参考答案](1)由题意得.B(.3).(3.1).∴直线的解析式为,直线与轴的交点为M(5.0).与轴的交点N(0.).设抛物线的解析式为.∵抛物线过点N.∴.∴.∴抛物线的解析式为=, (2)将△MON沿直线MN翻折.点O落在点P处.则P为(2.4).点P不在抛物线上, (3)若抛物线上下平移经过点.此时解析式为,当 时.∴.=.若抛物线向左平移经过点.平移距离为.此时解析式为=,若抛物线向右平移经过点.此时解析式为 [试题来源]09年南京中考模拟试卷
网址：http://m.1010jiajiao.com/timu_id_4424979[举报]
如图，在平面直角坐标系中，矩形OABC的顶点A（0，3），C（-1，0），将矩形OABC绕原点O顺时
针方向旋转90度，得矩形OA′B′C′矩形设直线BB’与x轴交于点M，与y轴交于点N，抛物线经过点C，M，N点．
解答下列问题：
（1）设直线BB′表示的函数解析式为y=mx+n，求m，n；
（2）求抛物线表示的二次函数的解析式；
（3）在抛物线上求出使S△PB′C′=S矩形OABC的所有点P的坐标． 查看习题详情和答案>>
针方向旋转90度，得矩形OA′B′C′矩形设直线BB’与x轴交于点M，与y轴交于点N，抛物线经过点C，M，N点．解答下列问题：
（1）设直线BB′表示的函数解析式为y=mx+n，求m，n；
（2）求抛物线表示的二次函数的解析式；
（3）在抛物线上求出使S△PB′C′=S矩形OABC的所有点P的坐标． 查看习题详情和答案>>
如图，在平面直角坐标系中，矩形OABC的顶点坐标为O（0，0），A（2
，0），B（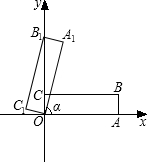
2
，2），把矩形OABC绕点O逆时针方向旋转α度，使点B正好落在y轴正半轴上，得到矩形OA1B1C1．
（1）求角α的度数；
（2）求直线A1B1的函数关系式，并判断直线A1B1是否经过点B，为什么？ 查看习题详情和答案>>
| 3 |
2| 3 |
（1）求角α的度数；
（2）求直线A1B1的函数关系式，并判断直线A1B1是否经过点B，为什么？ 查看习题详情和答案>>
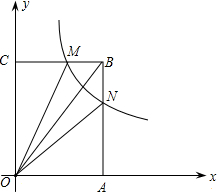
如图，在平面直角坐标系中，矩形OABC的顶点O为原点，E为AB上一点，把△CBE沿CE折叠，使点B恰好落在OA边上的点D处，点A，D的坐标分别为（5，0）和（3，0）．
（1）求点C的坐标；
（2）求DE所在直线的解析式；
（3）设过点C的抛物线y=2x2+
bx+c（b＜0）与直线BC的另一个交点为M，问在该抛物线
上是否存在点G，使得△CMG为等边三角形？若存在，求出点G的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）求点C的坐标；
（2）求DE所在直线的解析式；
（3）设过点C的抛物线y=2x2+
| 3 |
上是否存在点G，使得△CMG为等边三角形？若存在，求出点G的坐标；若不存在，请说明理由．
查看习题详情和答案>>
曲线y=
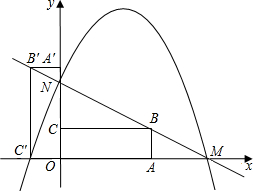列问题：