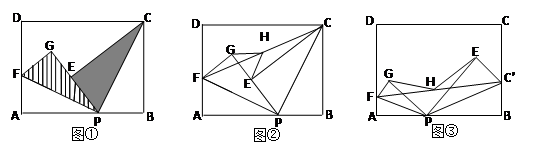
摘要:已知点P是矩形ABCD边AB上的任意一点(与点A.B不重合) (1)如图①.现将△PBC沿PC翻折得到△PEC,再在AD上取一点F.将△PAF沿PF翻折得到△PGF.并使得射线PE.PG重合.试问FG与CE的位置关系如何.请说明理由, 中.如图②.连接FC.取FC的中点H.连接GH.EH.请你探索线段GH和线段EH的大小关系.并说明你的理由, (3)如图③.分别在AD.BC上取点F.C’.使得∠APF=∠BPC’.与(1)中的操作相类似.即将△PAF沿PF翻折得到△PFG.并将△沿翻折得到△.连接.取的中点H.连接GH.EH.试问(2)中的结论还成立吗?请说明理由. [命题意图]综合考查图形变换的性质.逻辑推理能力以及探究能力 [参考答案](1)FG∥CE.在矩形ABCD中.∠A=∠B=90°.由题意得.∠G=∠A=90°.∠PEC=∠B=90°.∴∠GEC=90°.∴∠G=∠GEC.∴FG∥CE. (2)GH=EH.延长GH交CE于点M.由(1)得.FG∥CE.∴∠GFH=∠MCH.∵H为CF的中点.∴FH=CH.又∵∠GHF=∠MHC.∴△GFH≌△MHC.∴GH=HM=.∵∠GEC=90°.∴EH=.∴GH=EH. 中的结论还成立.取PF的中点M.的中点N.∵∠FGP=90°.M为PF的中点.∴..∥.∴GM=PM.∴∠GPF=∠MGP.∴∠GMF=∠GPF+∠MGP=2∠GPF.∵H为的中点.M为PF的中点.∴.同理..HN∥PF.∠.∴GM=HN.HM=EN.∵∠GPF=∠FPA..又.∴∠GPF=.∴∠GMF=∠.∵∥.HN∥PF.∴四边形HMPN为平行四边形.∴∠HMF=∠.∴∠GMH=∠HNE.∵GM=HN.HM=EN.∴△GMH≌△HNE.∴GH=HE. [试题来源]09大丰中考模拟试卷
网址:http://m.1010jiajiao.com/timu_id_4424978[举报]
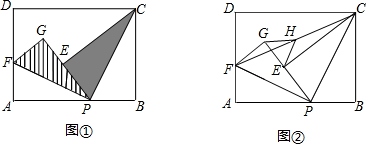
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由.
 查看习题详情和答案>>
查看习题详情和答案>>
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合).
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C′,使得∠APF=∠BPC′,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△PBC′沿PC′翻折得到△PEC′,连接FC′,取FC′的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.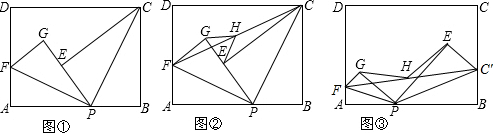 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C′,使得∠APF=∠BPC′,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△PBC′沿PC′翻折得到△PEC′,连接FC′,取FC′的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
【小题1】如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
【小题2】在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由.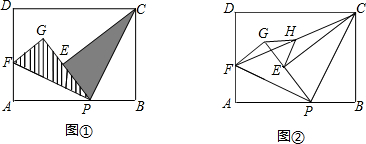 查看习题详情和答案>>
查看习题详情和答案>>
【小题1】如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
【小题2】在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由.
 查看习题详情和答案>>
查看习题详情和答案>>
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△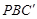 沿
沿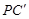 翻折得到△
翻折得到△ ,连接
,连接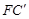 ,取
,取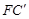 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.