摘要：4．已知直线+＝1(a.b是非零常数)与圆x2+y2＝100有公共点.且公共点的横坐标和纵坐标均为整数.那么这样的直线共有( ) A．60条 B．66条 C．72条 D．78条 答案:A 解析:在第一象限内圆x2+y2＝100上的整数点只有.而点在圆上. ∴圆x2+y2＝100上横.纵坐标的为整数的点共12个点． 过这12个点的圆x2+y2＝100的切线和割线共12+C＝78.而不合题意的过原点.斜率为0.斜率不存在的各6条． ∴共有78-3×6＝60条.故选A. 评析:考查排列组合的基础知识及分类讨论的思想.
网址：http://m.1010jiajiao.com/timu_id_4422813[举报]
已知椭圆
＋
＝1(a＞b＞0)的一个顶点为A(0,1)，离心率为
，
过点B(0，－2)及左焦点F1的直线交椭圆于C，D两点，右焦点设为F2.
(1)求椭圆的方程；
(2)求△CDF2的面积．
查看习题详情和答案>>已知双曲线
－
＝1(a＞0，b＞0)的右焦点为F，若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是(
)
A．[1,2] B．(1,2) C．[2，＋∞) D．(2，＋∞)
查看习题详情和答案>>
＋
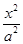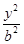＝1(a>b>0)的右焦点为F(3,0)，过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1，－1)，则E的方程为 (
)
＋
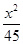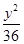＝1
B、
＋
＝1 
＋
＝1
D、
＋
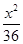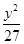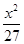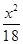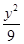＝1
＋
＝1(a>b>0)的左焦点为F，右顶点为A，点B在椭圆上，且BF⊥x轴，直线AB交y轴于点P.若
＝2
，则椭圆的离心率是（ ）
Ｂ．
Ｃ.
Ｄ.