摘要:函数的最值是指函数在给定的定义域区间上能否取到最大(小)值的问题.如果不注意定义域.将会导致最值的错误.如: 例2:求函数在[-2.5]上的最值. 解:∵ ∴ 当时. 初看结论.本题似乎没有最大值.只有最小值.产生这种错误的根源在于学生是按照求二次函数最值的思路.而没有注意到已知条件发生变化.这是思维呆板性的一种表现.也说明学生思维缺乏灵活性. 其实以上结论只是对二次函数在R上适用.而在指定的定义域区间上.它的最值应分如下情况: ⑴ 当时.在上单调递增函数, ⑵ 当时.在上单调递减函数, ⑶ 当时.在上最值情况是: . .即最大值是中最大的一个值. 故本题还要继续做下去: ∵ ∴ ∴ ∴ 函数在[-2.5]上的最小值是- 4.最大值是12. 这个例子说明.在函数定义域受到限制时.若能注意定义域的取值范围对函数最值的影响.并在解题过程中加以注意.便体现出学生思维的灵活性.
网址:http://m.1010jiajiao.com/timu_id_4419638[举报]
(2003•东城区二模)某城市为了改善交通状况,需进行路网改造.已知原有道路a个标段(注:1个标段是指一定长度的机动车道),拟增建x个标段的新路和n个道路交叉口,n与x满足关系n=ax+b,其中b为常数.设新建1个标段道路的平均造价为k万元,新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的β倍(β≥1),n越大,路网越通畅,记路网的堵塞率为μ,它与β的关系为μ=
.
(Ⅰ)写出新建道路交叉口的总造价y(万元)与x的函数关系式:
(Ⅱ)若要求路网的堵塞率介于5%与10%之间,而且新增道路标段为原有道路标段数的25%,求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围;
(Ⅲ)当b=4时,在(Ⅱ)的假设下,要使路网最通畅,且造价比P最高时,问原有道路标段为多少个?
查看习题详情和答案>>
| 1 | 2(1+β) |
(Ⅰ)写出新建道路交叉口的总造价y(万元)与x的函数关系式:
(Ⅱ)若要求路网的堵塞率介于5%与10%之间,而且新增道路标段为原有道路标段数的25%,求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围;
(Ⅲ)当b=4时,在(Ⅱ)的假设下,要使路网最通畅,且造价比P最高时,问原有道路标段为多少个?
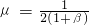 .
.