摘要：123．求曲线的切线时.关键点在何处?求函数图象上点处的切线方程的关键在于确定该点切线处的斜率.由导数的几何意义知.(注意曲线上某点处的导数值就是切线的斜率.故当存在时.切线方程为求曲线的切线要注意“过点的切线 与“点处的切线 的差异.过点的切线中.点不一定是切点.点也不一定在已知曲线上,点处的切线.点是切点.
网址：http://m.1010jiajiao.com/timu_id_4419601[举报]
有以下结论：
（1）椭圆、双曲线、抛物线和圆统称为圆锥曲线；
（2）微积分创立于十七世纪中叶，它的创立与求曲线的切线直接相关；
（3）若函数f（x）的导函数f'（x）=f（x），则f（x）=ex
其中正确的结论个数是（ ）
（1）椭圆、双曲线、抛物线和圆统称为圆锥曲线；
（2）微积分创立于十七世纪中叶，它的创立与求曲线的切线直接相关；
（3）若函数f（x）的导函数f'（x）=f（x），则f（x）=ex
其中正确的结论个数是（ ）
查看习题详情和答案>>
+ 
．
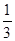
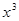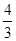的切线中，斜率最小的切线的方程。