摘要：114．在用圆锥曲线与直线联立求解时.消元后得到的方程中要注意:二次项的系数是否为零?判别式的限制．(求交点.弦长.中点.斜率.对称.存在性问题都在下进行).
网址：http://m.1010jiajiao.com/timu_id_4419592[举报]
在等差数列
中，
，
，其中
是数列的前
项之和，曲线
的方程是
，直线
的方程是
．
求数列的通项公式；
当直线与曲线相交于不同的两点
，
时，令
，
求
的最小值；
对于直线和直线外的一点P，用“上的点与点P距离的最小值”定义点P到直线的距离与原有的点到直线距离的概念是等价的，若曲线与直线不相交，试以类似的方式给出一条曲线与直线间“距离”的定义，并依照给出的定义，在中自行选定一个椭圆，求出该椭圆与直线的“距离”．
已知函数f（x）=ln（ex+1）-ax（a∈R）．
①若曲线y=f（x）在x=0处与直线x+y=b相切，求a，b的值；
②设x∈[-ln2，0]时，f（x）在x=0处取得最大值，求实数a的取值范围． 查看习题详情和答案>>
①若曲线y=f（x）在x=0处与直线x+y=b相切，求a，b的值；
②设x∈[-ln2，0]时，f（x）在x=0处取得最大值，求实数a的取值范围． 查看习题详情和答案>>
在直角坐标系XOY中，已知点A（1，0），B（-1，0），C（0，1），D（0，-1），动点M满足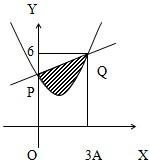
已知曲线y=x2-2x+3与直线y=x+3相交于点P（0，3）、Q（3，6）两点．