摘要:8.记住函数的几个重要性质: (1)关于对称性. 函数图象的对称轴和对称中心举例 函 数 满 足 的 条 件 对称轴 满足的函数的图象 [或] 满足的函数的图象 [或] 满足的函数的图象 满足的函数的图象 满足的函数的图象 满足的函数的图象 满足与的两个函数的图象 满足与的两个函数的图象 满足与的两个函数的图象 (2) 关于奇偶性与单调性的关系. ① 如果奇函数在区间上是递增的,那么函数在区间上也是递增的; ② 如果偶函数在区间上是递增的,那么函数在区间上是递减的; (3) 关于单调性. ①证明函数的单调性的方法为定义法和导数法. ②关于复合函数的单调性. 如果函数在区间上定义, 若为增函数, 为增函数,则为增函数; 若为增函数, 为减函数,则为减函数; 若为减函数, 为减函数,则为增函数; 若为减函数, 为增函数,则为减函数; ③关于分段函数的单调性. 若函数,在区间上是增函数, 在区间上是增函数,则在区间上不一定是增函数,若使得在区间上一定是增函数,需补充条件: (4) 关于图象变换. 平移 变 换 向左移个单位 向右移个单位 向上移个单位 向下移个单位 按向量平移 的图象→的图象 的图象→的图象 的图象→的图象 的图象→的图象 的图象→的图象 伸 缩 变 换 每点纵标伸倍 每点横标伸倍 的图象→的图象 的图象→的图象 绝对 值 变换 关于轴对称 将轴下方图象翻上 的图象→的图象 的图象→的图象 (5) 关于周期性. 函数的对称性与周期性的关系 函数关系() 周期 (6) 关于奇偶性. 20080515 ①判断函数的奇偶性,要注意定义域是否关于原点对称. ②若奇函数在处有定义,则;对于偶函数的定义常可用到下面的形式:. ③任何一个定义域关于原点对称的函数,总可以表示为一个奇函数和一个偶函数的和,其中. (7) 求函数的解析式,特别是解应用题的函数式时,一定要注明定义域. (8) 求方程或不等式的解集,或者求定义域,值域时,要按要求写成集合的形式.
网址:http://m.1010jiajiao.com/timu_id_4419485[举报]
下列是关于函数![]() 的几个命题:
的几个命题:
①若![]() 的一个零点;
的一个零点;
②若x0是![]() 上的零点,则可用二分法求x0的近似值;
上的零点,则可用二分法求x0的近似值;
③函数![]() 的零点是方程
的零点是方程![]() 的根,但
的根,但![]() 的根不一定是函数
的根不一定是函数![]() 的零点;
的零点;
④用二分法求方程的根时,得到的都是近似值.
以上叙述中,正确的个数为
A.0 B.1 C.3 D.4
查看习题详情和答案>>下列是关于函数![]() 的几个命题:
的几个命题:
①若![]() 的一个零点;
的一个零点;
②若x0是![]() 上的零点,则可用二分法求x0的近似值;
上的零点,则可用二分法求x0的近似值;
③函数![]() 的零点是方程
的零点是方程![]() 的根,但
的根,但![]() 的根不一定是函数
的根不一定是函数![]() 的零点;
的零点;
④用二分法求方程的根时,得到的都是近似值.
以上叙述中,正确的个数为
A.0 B.1 C.3 D.4
查看习题详情和答案>>6、下列是关于函数y=f(x),x∈[a,b]的几个命题:
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为( )
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为( )
查看习题详情和答案>>
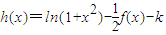 有几个零点?
有几个零点?