摘要：21．．在平面直角坐标系中.将A.D(3.1) 用线段依次连接起来形成一个图案. (1)直接写出图案①的面积: , (2)请按要求对图案作如下变换: a．将图案①绕点O逆时针旋转90°得到图案②, b．以点O为位似中心.位似比为2∶1将图案① 在位似中心的异侧进行放大得到图案③, (3)若图案①上某点P的坐标 为(a.b).图案②中与之对应的点为点Q.图 案③中与之对应的点为R.则S△PQR＝ ． [命题意图]几何变换.涉及旋转.位似等多种变换.为不同层次的学生进行分层设问.使得每一个学生都有较大的思维空间体现了课标中“数学教育面向全体学生 .“不同的学生在数学上得到不同的发展 的理念. [试题来源]2009淮阴模拟题 [参考答案](1)5,(2分 ) (2)如图:(4分) (3)(a2+b2) (4分)
网址：http://m.1010jiajiao.com/timu_id_4418714[举报]
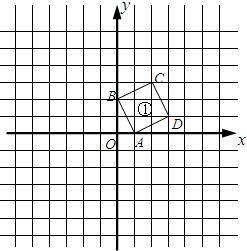在平面直角坐标系中，将A（1，0）、B（0，2）、C（2，3）、D（3，1）用线段依次连接起来形成一个图案（图案①）．将图案①绕点O逆时针旋转90°得到图案②；以点O为位似中心，位似比为1：2将图案①在位似中心的异侧进行放大得到图案③．（1）在坐标系中分别画出图案②和图案③；
（2）若点D在图案②中对应的点记为点E，在图案③中对应的点记为点F，则S△DEF=
（3）若图案①上任一点P（A、B除外）的坐标为（a，b），图案②中与之对应的点记为点Q，图案③中与之对应的点记为点R，则S△PQR=
在平面直角坐标系中，将抛物线y1=x2-4x+1向左平移3个单位长度，再向上平移4个单位长度，得到抛物线y2，然后将抛物线y2绕其顶点顺时针旋转180°，得到抛物线y3．
（1）求抛物线y2、y3的解析式．
（2）求y3＜0时，x的取值范围．
（3）判断以抛物线y3的顶点以及其与x轴的交点为顶点的三角形的形状，并求它的面积． 查看习题详情和答案>>
（1）求抛物线y2、y3的解析式．
（2）求y3＜0时，x的取值范围．
（3）判断以抛物线y3的顶点以及其与x轴的交点为顶点的三角形的形状，并求它的面积． 查看习题详情和答案>>
23、在平面直角坐标系中，将坐标是（0，4）、（1，0）、（2，4）、（3，0）、（4，4）的点用线段依次连接起来形成一个图案．（1）在下列坐标系中画出这个图案（图案①）；
（2）若将上述各点的横坐标保持不变，纵坐标分别乘以-1，再将所得的各点用线段依次连接起来，画出所得的图案（图案②）；
（3）若将上述各点的纵坐标保持不变，横坐标分别乘以-1，再将所得的各点用线段依次连接起来，画出所得的图案（图案③）；
（4）图案①与图案②有什么位置关系？图案②与图案③有什么位置关系．
次连接起来形成一个图案（图案①）．
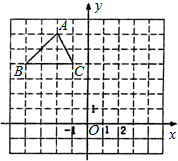标是