摘要:12.如图所示.甲船由A岛出发向北偏东45°的方向作匀速直线航行.速度为15海里/小时.在甲船从A岛出发的同时.乙船从A岛正南40海里处的B岛出发.朝北偏东θ的方向作匀速直线航行.速度为10海里/小时. (1)求出发后3小时两船相距多少海里? (2)求两船出发后多长时间距离最近?最近距离为多少海里? (3)两船在航行中能否相遇?试说明理由. [解析] 以A为原点.BA所在直线为y轴建立如图所示的平面直角坐标系.设在t时刻甲.乙两船分别在P(x1.y1).Q(x2.y2). 则. 由tan θ=可得.cos θ=.sin θ=. 故. (1)令t=3.P.Q两点的坐标分别为. |PQ|===5. 即出发后3小时两船相距5海里. 的解法过程易知: |PQ|= = ==≥20. ∴当且仅当t=4时.|PQ|取得最小值20. 即两船出发后4小时时距离最近.最近距离为20海里. (3)射线AP的方程为y=x(x≥0). 射线BQ的方程为y=2x-40(x≥0). 它们的交点为M.若甲.乙两船相遇.则应在M点处. 此时.|AM|==40. 甲船到达M点所用的时间为:t甲===. |BM|==40. 乙船到达M点所用的时间为:t乙==4. ∵t甲≠t乙.∴甲.乙两船不会相遇.
网址:http://m.1010jiajiao.com/timu_id_4417427[举报]
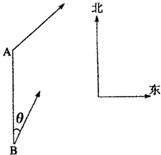 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
(Ⅰ)求4小时后甲船到B岛的距离为多少海里?
(Ⅱ)若两船能相遇,求m. 查看习题详情和答案>>
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
| 5 |
(1)求出发后3小时两船相距多少海里?
(2)求两船出发后多长时间距离最近?最近距离为多少海里?
(3)两船在航行中能否相遇,试说明理由. 查看习题详情和答案>>
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
(1)若两船能相遇,求m.
(2)当m=10
| 5 |
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ=
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ= )的方向作匀速直线航行,速度为m海里/小时.
)的方向作匀速直线航行,速度为m海里/小时. 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 海里/小时.
海里/小时.