摘要：(二)补集思想 有些圆锥曲线问题.从正面处理较难.常需分类讨论.运算量大.且讨论不全又容易出错.如用补集思想考虑其对立面.可以达到化繁为简的目的. [例2] 为何值时.直线:不能垂直平分抛物线的某弦. 解:设.直线垂直平分抛物线的某弦.若直线垂直平分抛物线的弦AB.且A.B.则. 上述两式相减得: 即 又设M是弦AB的中点.且.则 因为点M在直线上.所以 由于M在抛物线的内部.所以.即 故原命题中的取值范围是或
网址：http://m.1010jiajiao.com/timu_id_4413335[举报]
已知
之间的一组数据如表所示，对于表中数据，现在给出如下拟合直线，则根据最小二乘法思想判断拟合程度最好的直线是（ ）
|
|
2 |
3 |
4 |
5 |
6 |
|
|
3 |
4 |
6 |
8 |
9 |
A．
B．
C．
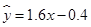D．
查看习题详情和答案>>
已知x，y之间的一组数据如表所示，对于表中数据，现在给出如下拟合直线，则根据最小二乘法思想判断拟合程度最好的直线是
[ ]
A．
＝x＋1
B．
＝2x－1
C．
＝1.6x－0.4
D．
＝1.5x
已知
之间的一组数据如表
所示，对于表中数据，现在给出如下拟合直线，则根据最小二乘法思想判断拟合程度最好的直线是（ ）
A．
B．
C．
D．
|
| 2 | 3 | 4 | 5 | 6 |
|
| 3 | 4 | 6 | 8 | 9 |
已知x，y之间的一组数据如下表：
对于表中数据，现给出如下拟合直线：①y=x+1；②y=2x-1；③y=
x-
；④y=
x，则根据最小二乘法的思想得拟合程度最好的直线是 （填序号）．
查看习题详情和答案>>
| x | 2 | 3 | 4 | 5 | 6 |
| y | 3 | 4 | 6 | 8 | 9 |
| 8 |
| 5 |
| 2 |
| 5 |
| 3 |
| 2 |