摘要:1?已知.斜边//平面.分别与平面成和的角.已知.试求到平面的距离 解:作于.于.则由.得 .且就是到平面的距离. 设.连结.则. ∴.在中.. ∴.∴.即到平面的距离为.2.已知棱长为a的正方体ABCD-A1B1C1D1.M.N分别是B1C1和C1D1的中点. ⑴求证:B1D1//平面CMN. ⑵求点B1到平面CMN的距离. 分析:显然有B1D1//MN.所以B1D1//平面CMN. ∴ 点B1到平面CMN的距离就是直线B1D1到平面CMN的距离. ∴ 可以考虑求B1D1的中点O到平面CMN的距离. 解:⑴∵ M.N分别是B1C1和C1D1的中点.∴ MN//B1D1. 而 MN平面CMN.B1D1平面CMN.∴ B1D1//平面CMN. ⑵连接AC.A1C1.A1C1交B1D1于O.交MN于E.则E是MN的中点.且MN⊥A1C1. ∵ AA1⊥平面A1B1C1D1.MN 平面CMN. ∴ AA1⊥MN. ∴ MN⊥平面A1ACC1. ∴ 平面CMN⊥平面A1ACC1. 在平面A1ACC1内作OH垂直于平面CMN和平面A1ACC1的交线CE于H.则OH⊥平面CMN. ∴ OH的长就是点O到平面CMN的距离. 由⑴知.OH的长就是点B1到平面CMN的距离. 由Rt△OHE∽Rt△CC1E可得.. ∵ .. . ∴ . ∴ 点B1到平面CMN的距离等于. 说明:①由于点B1在平面CMN内的射影不易作出.所以我们就把点B1平移到点O.作出点O在平面CMN内的射影H.从而求出点B1到平面CMN的距离.这是处理点到平面的距离问题的常用手段. ②对于直线到平面的距离问题.一般取直线上的特殊点向平面上做垂线.
网址:http://m.1010jiajiao.com/timu_id_4411459[举报]
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
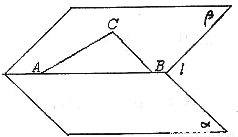
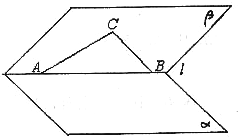 如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.
如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.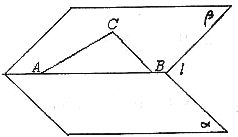 如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.
如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.