摘要:3.函数是奇函数.只需讨论函数在(0.1)上的单调性 当时. 若.则.函数在(0.1)上是减函数, 若.则.函数在(0.1)上是增函数. 又函数是奇函数.而奇函数在对称的两个区间上有相同的单调性.所以当时.函数在上是减函数.当时.函数在上是增函数. 说明:分类讨论是重要的数学解题方法.它把数学问题划分成若干个局部问题.在每一个局部问题中.原先的“不确定因素 不再影响问题的解决.当这些局部问题都解决完时.整个问题也就解决了.在判断含参数函数的单调性时.不仅要考虑到参数的取值范围.而且要结合函数的定义域来确定的符号.否则会产生错误判断. 分类讨论必须给予足够的重视.真正发挥数学解题思想作为联系知识与能力中的作用.从而提高简化计算能力. 利用导数求函数的单调区间 例 求下列函数的单调区间:
网址:http://m.1010jiajiao.com/timu_id_4410652[举报]
(理科)函数y=x+
(a是常数,且a>0)有如下性质:①函数是奇函数;②函数在(0,
]上是减函数,在[
,+∞)上是增函数.
(1)如果函数y=x+
(x>0)的值域是[6,+∞),求b的值;
(2)判断函数y=x2+
(常数c>0)在定义域内的奇偶性和单调性,并加以证明;
(3)对函数y=x+
和y=x2+
(常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).
查看习题详情和答案>>
| a |
| x |
| a |
| a |
(1)如果函数y=x+
| 2b |
| x |
(2)判断函数y=x2+
| c |
| x2 |
(3)对函数y=x+
| a |
| x |
| c |
| x2 |
下列命题正确的是 (只须填写命题的序号即可)
(1)函数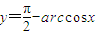 是奇函数;
是奇函数;
(2)在△ABC中,A+B<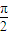 是sinA<cosB的充要条件;
是sinA<cosB的充要条件;
(3)当α∈(0,π)时,cosα+sinα=m(0<m<1),则α一定是钝角,且|tanα|>1;
(4)要得到函数y=cos(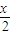 -
- )的图象,只需将y=sin
)的图象,只需将y=sin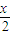 的图象向左平移
的图象向左平移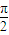 个单位.
查看习题详情和答案>>
个单位.
查看习题详情和答案>>
(1)函数
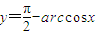 是奇函数;
是奇函数;(2)在△ABC中,A+B<
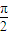 是sinA<cosB的充要条件;
是sinA<cosB的充要条件;(3)当α∈(0,π)时,cosα+sinα=m(0<m<1),则α一定是钝角,且|tanα|>1;
(4)要得到函数y=cos(
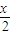 -
- )的图象,只需将y=sin
)的图象,只需将y=sin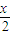 的图象向左平移
的图象向左平移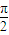 个单位.
查看习题详情和答案>>
个单位.
查看习题详情和答案>>
(理科)函数 有如下性质:①函数是奇函数;②函数在
有如下性质:①函数是奇函数;②函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
(1)如果函数 (x>0)的值域是[6,+∞),求b的值;
(x>0)的值域是[6,+∞),求b的值;
(2)判断函数 (常数c>0)在定义域内的奇偶性和单调性,并加以证明;
(常数c>0)在定义域内的奇偶性和单调性,并加以证明;
(3)对函数 (常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).
(常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).
查看习题详情和答案>>
 有如下性质:①函数是奇函数;②函数在
有如下性质:①函数是奇函数;②函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.(1)如果函数
 (x>0)的值域是[6,+∞),求b的值;
(x>0)的值域是[6,+∞),求b的值;(2)判断函数
 (常数c>0)在定义域内的奇偶性和单调性,并加以证明;
(常数c>0)在定义域内的奇偶性和单调性,并加以证明;(3)对函数
 (常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).
(常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).查看习题详情和答案>>
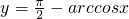 是奇函数;
是奇函数; 是sinA<cosB的充要条件;
是sinA<cosB的充要条件; -
- )的图象,只需将y=sin
)的图象,只需将y=sin