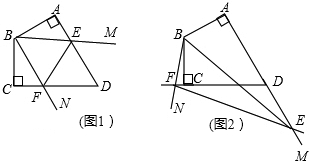
摘要： 证明:(1)在中.分别是的中点 且 又是的中点.. 且 四边形是平行四边形 (2)证明:分别是的中点 且 又.且..且 平行四边形是正方形． 在梯形ABCD中.AB∥CD.∠A=90°. AB=2.BC=3.CD=1.E是AD中点． 求证:CE⊥BE． 证明: 过点C作CF⊥AB.垂足为F． ∵ 在梯形ABCD中.AB∥CD.∠A=90°. ∴ ∠D＝∠A＝∠CFA＝90°． ∴四边形AFCD是矩形． AD=CF, BF=AB-AF=1． 在Rt△BCF中. CF2=BC2-BF2=8. ∴ CF=． ∴ AD=CF=． ∵ E是AD中点. ∴ DE=AE=AD=． 在Rt△ABE和 Rt△DEC中. EB2=AE2+AB2=6. EC2= DE2+CD2=3. EB2+ EC2=9=BC2． ∴ ∠CEB＝90°． ∴ EB⊥EC．
网址：http://m.1010jiajiao.com/timu_id_4410143[举报]
由四边形各边中点组成的四边形称为“中点四边形”．如图，在四边形ABCD中，已知E、F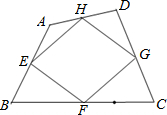
、G、H分别是边AB、BC、CD、DA各边的中点．
（1）观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在（1）的条件下，当对角线AC=BD时，中点四边形EFGH的形状又是什么呢？请说明理由．
（3）直接写出：①菱形ABCD的中点四边形EFGH的形状是 ；
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是 ．
查看习题详情和答案>>
、G、H分别是边AB、BC、CD、DA各边的中点．（1）观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在（1）的条件下，当对角线AC=BD时，中点四边形EFGH的形状又是什么呢？请说明理由．
（3）直接写出：①菱形ABCD的中点四边形EFGH的形状是
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是
由四边形各边中点组成的四边形称为“中点四边形”．如图，在四边形ABCD中，已知E、F
、G、H分别是边AB、BC、CD、DA各边的中点．
（1）观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在（1）的条件下，当对角线AC=BD时，中点四边形EFGH的形状又是什么呢？请说明理由．
（3）直接写出：①菱形ABCD的中点四边形EFGH的形状是______；
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是______．
查看习题详情和答案>>
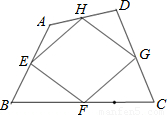
由四边形各边中点组成的四边形称为“中点四边形”．如图，在四边形ABCD中，已知E、F、G、H分别是边AB、BC、CD、DA各边的中点．
（1）观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在（1）的条件下，当对角线AC=BD时，中点四边形EFGH的形状又是什么呢？请说明理由．
（3）直接写出：①菱形ABCD的中点四边形EFGH的形状是______；
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是______．
查看习题详情和答案>>
（1）观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在（1）的条件下，当对角线AC=BD时，中点四边形EFGH的形状又是什么呢？请说明理由．
（3）直接写出：①菱形ABCD的中点四边形EFGH的形状是______；
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是______．
查看习题详情和答案>>
