摘要: 已知锐角△ABC中.sin(A+B)=.sin(A-B)=. (1)求证:tanA=2tanB, (2)设AB=3.求AB边上的高. 剖析:有两角的和与差联想到两角和与差的正弦公式.结合图形.以. (1)证明:∵sin(A+B)=.sin(A-B)=. ∴ =2. ∴tanA=2tanB. (2)解:<A+B<π.∴sin(A+B)=. ∴tan(A+B)=-. 即=-.将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0.解得tanB=.得tanB=.∴tanA=2tanB=2+. 设AB边上的高为CD.则AB=AD+DB=+=.由AB=3得CD=2+.所以AB边上的高为2+. 评述:本题主要考查三角函数概念.两角和与差的公式以及应用.分析和计算能力.
网址:http://m.1010jiajiao.com/timu_id_4410026[举报]
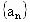 满足
满足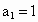 ,
,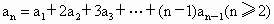 ,则
,则
 上的动点,则点P到直线3x-4y-10=0的距离的最小值为__________.
上的动点,则点P到直线3x-4y-10=0的距离的最小值为__________. ,则下列各式中错误的是
,则下列各式中错误的是
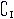 A)∪B=I
A)∪B=I
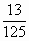
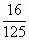
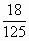

 ,点O(0,0)和A(1,-2)在l上的射影分别是
,点O(0,0)和A(1,-2)在l上的射影分别是 和
和 ,则
,则 ,其中λ等于
,其中λ等于

