摘要：若满足 A.2005
网址：http://m.1010jiajiao.com/timu_id_4407185[举报]
(2005
广东，17)在平面直角坐标系xOy中，抛物线
上异于坐标原点O的两不同动点A、B，满足AO⊥BO(如图所示)．
(1)
求△AOB的重心G(即三角形三条中线的交点)的轨迹方程；(2)
△AOB的面积是否存在最小值?若存在，请求出最小值；若不存在，请说明理由．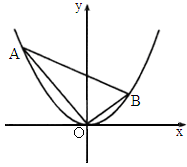
（2005•东城区一模）已知O为坐标原点，点E、F的坐标分别为（-1，0）和（1，0），点A、P、Q运动时满足|
|=2|
|，
=
，
•
=0，
∥
．
（1）求动点P的轨迹C的方程；
（2）设M、N是C上两点，若
+2
=3
，求直线MN的方程．
查看习题详情和答案>>
| AE |
| EF |
| AQ |
| QF |
| PQ |
| AF |
| AP |
| EP |
（1）求动点P的轨迹C的方程；
（2）设M、N是C上两点，若
| OM |
| ON |
| OE |
（2005•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
（2）若三角形有一个内角为arccos
，周长为定值p，求面积S的最大值；
（3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
absinC≤
×9×8sinC=36sinC，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
，sinC=
，所以，该三角形面积的最大值是
．以上解答是否正确？若不正确，请你给出正确的解答．
查看习题详情和答案>>
（2）若三角形有一个内角为arccos
| 7 |
| 9 |
（3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
| 1 |
| 2 |
| 1 |
| 2 |
| 43 |
| 48 |
| ||
| 48 |
3
| ||
| 4 |
的直线l过点(0，
)和椭圆C：
(a＞b＞0)的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上．
．若存在，求直线m的方程；若不存在，请说明理由．
