摘要： 对于个向量.若存在个不全为零的实数使得 成立.则称向量是线性相关的.按此规定.能使向量是线性相关的实数的值依次为 .根据线性相关的定义得.令则..∴的一组值为-4.2.1
网址：http://m.1010jiajiao.com/timu_id_4399485[举报]
对于n个向量
，
，
…
，若存在n个不全为零的实数k1，k2，…kn，使得：k1
+k2
+k3
+…+kn
=0成立，则称向量
，
，
…
是线性相关的．按此规定，能使向量
=(1，0)，
=(1，-1)，
=(2，2)是线性相关的实数为k1，k2，k3，则k1+4k3= ．
查看习题详情和答案>>
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
对于n个向量
，
，
…
，若存在n个不全为零的实数k1，k2，…kn，使得：k1
+k2
+k3
+…+kn
=0成立，则称向量
，
，
…
是线性相关的．按此规定，能使向量
=(1，0)，
=(1，-1)，
=(2，2)是线性相关的实数为k1，k2，k3，则k1+4k3=______．
查看习题详情和答案>>
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
| an |
| a1 |
| a2 |
| a3 |
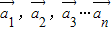，若存在n个不全为零的实数k1，k2，…kn，使得：
成立，则称向量
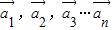是线性相关的．按此规定，能使向量
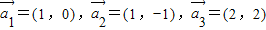是线性相关的实数为k1，k2，k3，则k1+4k3= ．
，…，
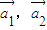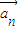，若存在n个不全为零的实数k1，k2，…kn，使得k1
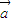1+k2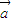
2+…+kn
n=0成立，则称向量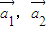
，…，
，是线性相关的．按此规定，能使向量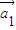
=（1，0），
=（1，-1），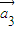
=（2，2）是线性相关的实数k1，k2，k3的值依次为 ．（只需写出一组值即可）
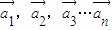，若存在n个不全为零的实数k1，k2，…kn，使得：
成立，则称向量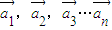
是线性相关的．按此规定，能使向量
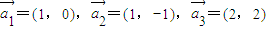是线性相关的实数为k1，k2，k3，则k1+4k3= ．