摘要:由题意得即. ------3
网址:http://m.1010jiajiao.com/timu_id_430273[举报]
解析:依题意得f(x)的图象关于直线x=1对称,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函数f(x)是以4为周期的函数.由f(x)在[3,5]上是增函数与f(x)的图象关于直线x=1对称得,f(x)在[-3,-1]上是减函数.又函数f(x)是以4为周期的函数,因此f(x)在[1,3]上是减函数,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
查看习题详情和答案>>拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
倍”,请你写出此命题在立体几何中类似的真命题:
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
.(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
| ||
| 2 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
| ||
| 3 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
.
| ||
| 3 |
拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______.
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
倍”,请你写出此命题在立体几何中类似的真命题:______.
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______.
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
| ||
| 2 |
拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______.
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的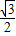 倍”,请你写出此命题在立体几何中类似的真命题:______
查看习题详情和答案>>
倍”,请你写出此命题在立体几何中类似的真命题:______
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______.
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
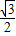 倍”,请你写出此命题在立体几何中类似的真命题:______
查看习题详情和答案>>
倍”,请你写出此命题在立体几何中类似的真命题:______
查看习题详情和答案>>
设点 是抛物线
是抛物线
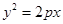
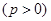 的焦点,
的焦点,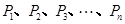 是抛物线
是抛物线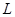 上的
上的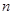 个不同的点(
个不同的点(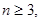
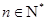 ).
).
(1) 当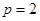 时,试写出抛物线
时,试写出抛物线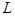 上的三个定点
上的三个定点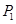 、
、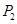 、
、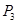 的坐标,从而使得
的坐标,从而使得
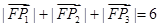 ;
;
(2)当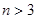 时,若
时,若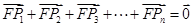 ,
,
求证: ;
;
(3) 当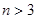 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则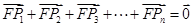 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数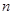 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
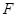 是抛物线
是抛物线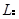
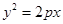
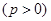 的焦点,
的焦点,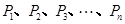 是抛物线
是抛物线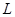 上的
上的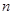 个不同的点(
个不同的点(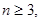
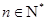 ).
).(1) 当
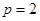 时,试写出抛物线
时,试写出抛物线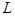 上的三个定点
上的三个定点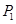 、
、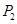 、
、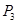 的坐标,从而使得
的坐标,从而使得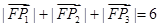 ;
;(2)当
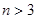 时,若
时,若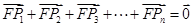 ,
,求证:
 ;
;(3) 当
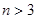 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:“若
 ,则
,则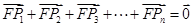 .”
.”开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数
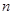 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.