摘要:(2)S△DPQ=t2-3t+30=.当t=6时.S△DPQ最小.此时BQ=3.
网址:http://m.1010jiajiao.com/timu_id_429735[举报]
下列各式从左边到右边的变形中,是因式分解的有( )
①24x2y=4x•6xy;②
ax+
bx=
x(a+b);③(x+4)(x-4)=x2-16;④25y2-10y+1=5y(5y-2)+1;⑤t2-3t+2=(t-1)(t-2);⑥x2+1=x(x+
).
①24x2y=4x•6xy;②
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
查看习题详情和答案>>
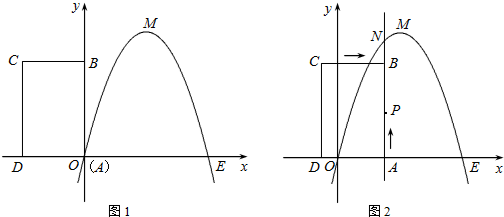
如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)直接写出该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以每秒1个单位长度的速度从A点出发沿射线AB匀速移动,设它们运动的时间为t秒(t>0),直线AB与该抛物线的交点为N(如图2所示).
①填空:当0<t≤3时,PN=
②在运动的过程中,以P、N、C、D为顶点的四边形能否成为平行四边形?若能,请求出此时t的值,若不能,请说明理由.
③设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最小值?为什么?
查看习题详情和答案>>
(1)直接写出该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以每秒1个单位长度的速度从A点出发沿射线AB匀速移动,设它们运动的时间为t秒(t>0),直线AB与该抛物线的交点为N(如图2所示).
①填空:当0<t≤3时,PN=
-t2+3t
-t2+3t
.(用含t的代数式表示);②在运动的过程中,以P、N、C、D为顶点的四边形能否成为平行四边形?若能,请求出此时t的值,若不能,请说明理由.
③设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最小值?为什么?
