网址:http://m.1010jiajiao.com/timu_id_428593[举报]
某工厂在“减员增效”工作中,规定下岗人员第一年可以到原单位领取全额工资,从第二年起,以后每年只能在原单位按上一年工资额的![]() 领取.该工厂根据下岗人员特长,创办新的经济实体.该实体预计第一年属投资阶段,没有利润,因而职员均无收入.第二年每人年收入可达b元,从第三年起每人年收入可在上一年的基础上递增
领取.该工厂根据下岗人员特长,创办新的经济实体.该实体预计第一年属投资阶段,没有利润,因而职员均无收入.第二年每人年收入可达b元,从第三年起每人年收入可在上一年的基础上递增![]() .如果某工人下岗后立即转入这个创办的经济实体,又设该工人下岗前的年工资额为a元.
.如果某工人下岗后立即转入这个创办的经济实体,又设该工人下岗前的年工资额为a元.
①求这位工人下岗后第n年的年收入an的表达式;
②当![]() 时,这位工人哪一年的年收入最少?最少年收入是多少?
时,这位工人哪一年的年收入最少?最少年收入是多少?
已知函数 ,
, .
.
(Ⅰ)若函数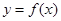 依次在
依次在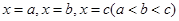 处取到极值.求
处取到极值.求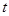 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的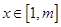 ,不等式
,不等式
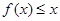 恒成立.求正整数
恒成立.求正整数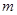 的最大值.
的最大值.
【解析】第一问中利用导数在在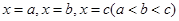 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的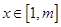 ,不等式
,不等式
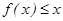 恒成立转化为
恒成立转化为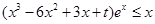 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式 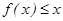 ,即
,即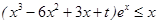 ,即
,即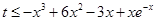 .
.
转化为存在实数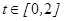 ,使对任意的
,使对任意的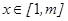 ,不等式
,不等式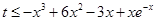 恒成立.
恒成立.
即不等式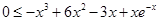 在
在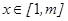 上恒成立.
上恒成立.
即不等式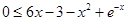 在
在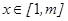 上恒成立.
上恒成立.
设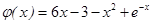 ,则.
,则.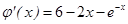
设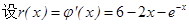 ,则
,则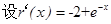 ,因为
,因为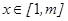 ,有
,有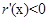 .
.
故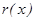 在区间
在区间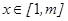 上是减函数。又
上是减函数。又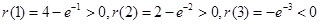
故存在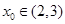 ,使得
,使得 .
.
当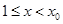 时,有
时,有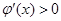 ,当
,当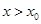 时,有
时,有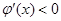 .
.
从而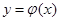 在区间
在区间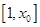 上递增,在区间
上递增,在区间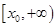 上递减.
上递减.
又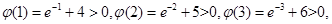 [来源:]
[来源:]
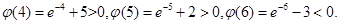
所以当 时,恒有
时,恒有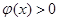 ;当
;当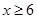 时,恒有
时,恒有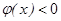
 ;
;
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>
设函数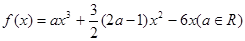
(1)当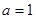 时,求曲线
时,求曲线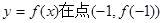 处的切线方程;
处的切线方程;
(2)当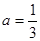 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间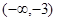 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
【解析】(1)中,先利用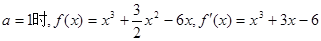 ,表示出点
,表示出点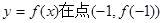 的斜率值
的斜率值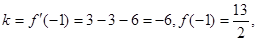 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当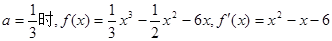 ,再令
,再令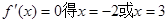 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间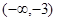 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当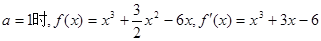 ……2分
……2分
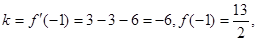 ∴
∴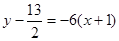
即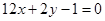 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当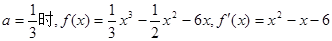
令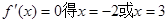 ………………6分
………………6分
∴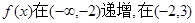 递减,在(3,+
递减,在(3,+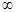 )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)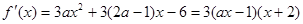
①若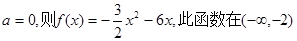 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
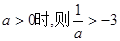 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数 的取值范围是
的取值范围是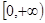
查看习题详情和答案>>
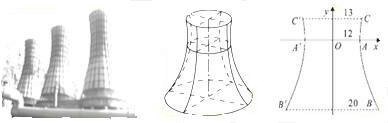

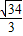 ,试求冷却塔的高应当设计为多少?
,试求冷却塔的高应当设计为多少?