摘要:故S△EAC=EO?AC=a2.(Ⅱ)由题设ABCD―A1B1C1D1是正四棱柱.得A1A⊥底面AC.A1A⊥AC.又A1A⊥A1B1. ∴A1A是异面直线A1B1与AC间的公垂线.∵D1B∥面EAC.且面D1BD与面EAC交线为EO.∴D1B∥EO.又O是DB的中点∴E是D1D的中点.D1B=2EO=2a.
网址:http://m.1010jiajiao.com/timu_id_425228[举报]
若α=tan100°,b=tan25°,c=tan55°,则a、b、c之间应有关系
- A.a+b+c=abc
- B.ab+bc+ac=1
- C.ab+bc+ac=a+b+c
- D.ab+bc+ac=a2+b2+c2
已知函数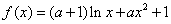 .
.
(Ⅰ)讨论函数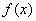 的单调性;
的单调性;
(Ⅱ)设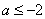 ,证明:对任意
,证明:对任意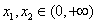 ,
,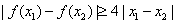 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
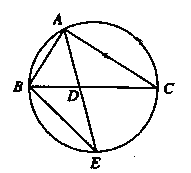
如图, 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点
(Ⅰ)证明: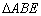 ∽△
∽△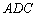 ;
;
(Ⅱ)若 的面积
的面积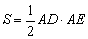 ,求
,求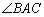 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
查看习题详情和答案>>
 AB,N为AB
AB,N为AB 上一点,
上一点,
 的大小。
的大小。