摘要:即通项公式an=4n-2.(Ⅲ)令cn=bn-1.
网址:http://m.1010jiajiao.com/timu_id_422798[举报]
 (2013•松江区一模)已知递增的等差数列{an}的首项a1=1,且a1、a2、a4成等比数列.
(2013•松江区一模)已知递增的等差数列{an}的首项a1=1,且a1、a2、a4成等比数列.(1)求数列{an}的通项公式an;
(2)设数列{cn}对任意n∈N*,都有
| c1 |
| 2 |
| c2 |
| 22 |
| cn |
| 2n |
(3)在数列{dn}中,d1=1,且满足
| dn |
| dn+1 |
(2013•松江区一模)已知递增的等差数列{an}的首项a1=1,且a1、a2、a4成等比数列.
(1)求数列{an}的通项公式an;
(2)设数列{cn}对任意n∈N*,都有
+
+…+
=an+1成立,求c1+c2+…+c2012的值.
(3)若bn=
(n∈N*),求证:数列{bn}中的任意一项总可以表示成其他两项之积.
查看习题详情和答案>>
(1)求数列{an}的通项公式an;
(2)设数列{cn}对任意n∈N*,都有
| c1 |
| 2 |
| c2 |
| 22 |
| cn |
| 2n |
(3)若bn=
| an+1 |
| an |
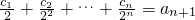 成立,求c1+c2+…+c2012的值.
成立,求c1+c2+…+c2012的值.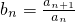 (n∈N*),求证:数列{bn}中的任意一项总可以表示成其他两项之积.
(n∈N*),求证:数列{bn}中的任意一项总可以表示成其他两项之积.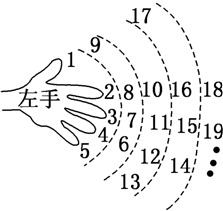 15、“欢欢”按如图所示的规则练习数数,记在数数过程中对应中指的数依次排列所构成的数列为{an},则数到2 008时对应的指头是
15、“欢欢”按如图所示的规则练习数数,记在数数过程中对应中指的数依次排列所构成的数列为{an},则数到2 008时对应的指头是