摘要：(Ⅰ)解:因为{cn+1-pcn}是等比数列.故有(cn+1-pcn)2＝(cn+2-pcn+1)(cn-pcn-1).将cn＝2n+3n代入上式.得［2n+1+3n+1-p(2n+3n)］2＝［2n+2+3n+2-p(2n+1+3n+1)］?［2n+3n-p(2n-1+3n-1)］即［(2-p)2n+(3-p)3n］2＝［(2-p)2n+1+(3-p)3n+1］［(2-p)2n-1+(3-p)3n-1］.
网址：http://m.1010jiajiao.com/timu_id_422626[举报]
已知函数y=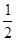
cos2x+
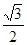sinxcosx+1,x∈R.
（1）求函数
的最小正周期；
（2）求函数的单调减区间.
【解析】第一问中利用化为单一三角函数y=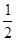sin(2x+
)+
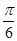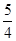.，然后利用周期公式求解得到。第二问中，2x+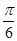落在正弦函数的增区间里面，解得的x的范围即为所求，
解：因为y=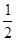cos2x+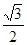sinxcosx+1,x∈R.所以y=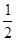sin(2x+)+.
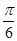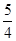(1)周期为T=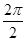
=π，
（2） 
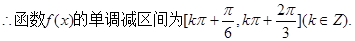
查看习题详情和答案>>
已知（x+1）（2-x）≥0的解为条件p，关于x的不等式x2+mx-2m2-3m-1＜0（m＞-
）的解为条件q．
（1）若p是q的充分不必要条件时，求实数m的取值范围．
（2）若￢p是￢q的充分不必要条件时，求实数m的取值范围．
查看习题详情和答案>>
| 2 | 3 |
（1）若p是q的充分不必要条件时，求实数m的取值范围．
（2）若￢p是￢q的充分不必要条件时，求实数m的取值范围．
给出下列命题：
①当a≥1时，不等式|x-4|+|x-3|＜a的解集非空
②存在一圆与直线系xcosθ+ysinθ=1（x∈R）都相切
③已知（x+2）2+
=1，则x2+y2的取值范围是[1，
]
④底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．
⑤函数y=f（x+2）和y=f（2-x）的图象关于直线x=2对称．
其中正确的有 ． 查看习题详情和答案>>
①当a≥1时，不等式|x-4|+|x-3|＜a的解集非空
②存在一圆与直线系xcosθ+ysinθ=1（x∈R）都相切
③已知（x+2）2+
=1，则x2+y2的取值范围是[1，]④底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．
⑤函数y=f（x+2）和y=f（2-x）的图象关于直线x=2对称．
其中正确的有 ． 查看习题详情和答案>>
）的解为条件q．