摘要:中的抛物线上有一个动点P.当点P在该抛物线上滑动到什么位置时,满足,并求出此时P点的坐标,中的抛物线交y轴于C点.在该抛物线的对称轴上是否存在点Q.使得△QAC的周长最小?若存在.求出Q点的坐标,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_419890[举报]
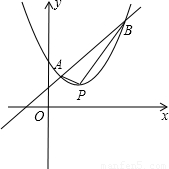
已知抛物线y=x2+bx+c与直线y=x+1有两个交点A、B.
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2
,求c的最小值,并写出c取最小值时抛物线的解析式;
(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时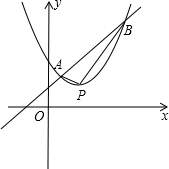 点P的坐标(t,T)满足的关系,若不存在说明理由.
查看习题详情和答案>>
点P的坐标(t,T)满足的关系,若不存在说明理由.
查看习题详情和答案>>
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2
| 2 |
(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2
| 2 |
②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时
 点P的坐标(t,T)满足的关系,若不存在说明理由.
查看习题详情和答案>>
点P的坐标(t,T)满足的关系,若不存在说明理由.
查看习题详情和答案>>
已知抛物线y=x2+bx+c与直线y=x+1有两个交点A、B.
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2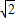 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;
(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2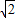 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时点P的坐标(t,T)满足的关系,若不存在说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2
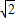 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2
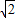 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时点P的坐标(t,T)满足的关系,若不存在说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
已知抛物线y=x2+bx+c与直线y=x+1有两个交点A、B.
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2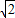 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;
(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2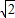 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时点P的坐标(t,T)满足的关系,若不存在说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)当AB的中点落在y轴时,求c的取值范围;
(2)当AB=2
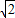 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;(3)设点P(t,T)在AB之间的一段抛物线上运动,S(t)表示△PAB的面积.
①当AB=2
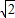 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;②当AB=m(正常数)时,S(t)是否仍有最大值,若存在,求出S(t)的最大值以及此时点P的坐标(t,T)满足的关系,若不存在说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;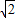 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;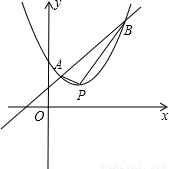
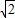 ,求c的最小值,并写出c取最小值时抛物线的解析式;
,求c的最小值,并写出c取最小值时抛物线的解析式;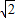 ,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;
,且抛物线与直线的一个交点在y轴时,求S(t)的最大值,以及此时点P的坐标;