摘要:又.所以P在以A.B为焦点的双曲线的左支上.且
网址:http://m.1010jiajiao.com/timu_id_4190[举报]
在△ABC中,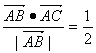 ,
,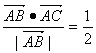 ,又E点在BC边上,且满足
,又E点在BC边上,且满足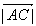 ,以A、B为焦点的双曲线经过C、E两点.
,以A、B为焦点的双曲线经过C、E两点.
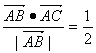 ,
,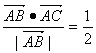 ,又E点在BC边上,且满足
,又E点在BC边上,且满足(1)求此双曲线的方程;
(2)设P是此双曲线上任意一点,过A点作∠APB平分线的垂线,垂足为M,求M点的轨迹方程.
查看习题详情和答案>>
在直角坐标系xoy中,已知三点A(-1,0),B(1,0),C(-1,
);以A、B为焦点的椭圆经过C点,
(1)求椭圆方程;
(2)设点D(0,1),是否存在不平行于x轴的直线l,与椭圆交于不同的两点M、N,使(
+
)•
=0?
若存在.求出直线l斜率的取值范围;
(3)对于y轴上的点P(0,n)(n≠0),存在不平行于x轴的直线l与椭圆交于不同两点M、N,使(
+
)•
=0,试求实数n的取值范围.
查看习题详情和答案>>
| 3 |
| 2 |
(1)求椭圆方程;
(2)设点D(0,1),是否存在不平行于x轴的直线l,与椭圆交于不同的两点M、N,使(
| PM |
| PN |
| MN |
若存在.求出直线l斜率的取值范围;
(3)对于y轴上的点P(0,n)(n≠0),存在不平行于x轴的直线l与椭圆交于不同两点M、N,使(
| PM |
| PN |
| MN |
点P在以F1,F2为焦点的双曲线E:
-
=1(a>0,b>0)上,已知PF1⊥PF2,|PF1|=2|PF2|,O为坐标原点.
(Ⅰ)求双曲线的离心率e;
(Ⅱ)过点P作直线分别与双曲线渐近线相交于P1,P2两点,且
•
=-
,2
+
=
,求双曲线E的方程;
(Ⅲ)若过点Q(m,0)(m为非零常数)的直线l与(2)中双曲线E相交于不同于双曲线顶点的两点M、N,且
=λ
(λ为非零常数),问在x轴上是否存在定点G,使
⊥(
-λ
)?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求双曲线的离心率e;
(Ⅱ)过点P作直线分别与双曲线渐近线相交于P1,P2两点,且
| OP1 |
| OP2 |
| 27 |
| 4 |
| PP1 |
| PP2 |
| 0 |
(Ⅲ)若过点Q(m,0)(m为非零常数)的直线l与(2)中双曲线E相交于不同于双曲线顶点的两点M、N,且
| MQ |
| QN |
| F1F2 |
| GM |
| GN |
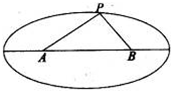 如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm.
如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm.