网址：http://m.1010jiajiao.com/timu_id_40903[举报]
一、二选择题：（34分）
1
2
3
4
5
6
7
8
9
10
B
A
A
C
C
D
AD
BC
ABC
BD
三、填空题（每小题4分，共8分）
11、 9 ， 12 。
12、0 ，
四、实验题（13题9分，14题8分，共17分）
13、（3）
――――――――――――――――3分
14、（1） D ； ――――――――――――――――2分
（2）弹簧压缩的长度
，滑块滑行的距离s，弹簧悬挂滑块时伸长的长度
，（3分）
（3）
/2s ――――――――――――――――3分
五、计算题（15题6分，16题11分）
15、解：以甲为参照物，乙相对甲的速度v=
=10（m/s），――3分
与AB方向的夹角为
，最小距离
=
Sin=60（m）――1分
乙走过的距离为
=Cos=80（m），t=/v=8（s）――2分
16、解：（1）由动能定理qE
－2mgR=0，――2分
qE=
mg――1分
∴=4R――1分
（2）设小环在A点的速度为
，由动能定理
qE（+R）－mgR=m
，（3分）=
，（1分）由向心力公式
N－qB－qE=m
，（2分）N=
mg+qB （1分）
17、解：（1）CD――4分
（2）选玻璃泡A内一定量的气体为研究对象，对于B管的体积略去不计，温度变化时A内气体经历的是一个等容过程――2分
玻璃泡A内气体的初始状态：
=300K，
=（76－16）cmHg=60cmHg
末状态：
=273K，
=？
由查理定律得：P=
=
×60cmHg=54。6cmHg――4分
所以t=
C时水银面高度，即刻度线的位置是
=（76－54。6）cm=21。
18、解：（1）设
为氚核速度，
为α粒子速度，
、
、
分别代表中子、氚核、氦核质量，反应前后动量守恒有：
=+――――――――――――――――――3分
代入数值可解得：=－1。0×
m/s，方向与反向――1分
（2）
和
在磁场中均受洛仑兹力，做匀速圆周运动由qvB=m
有：r=
――――――――――――――――――――2分
则它们做匀速圆周运动的轨道半径之比为：
：
=
：
=3：40――――――――――――2分
（3）和做匀速圆周运动的周期之比为：
：
=
：
=3：2―――――――――――2分
所以它们的旋转周数之比：
：
=：=2：3，即转3周时，转2周
――――――――――2分
海南侨中2008届物理科第一次模拟考试题
答题卷
三、填空题（共2小题，8分）
11、 ， 。
12、 ， 。
四、实验题（共2小题，17分）
13、
（3） 。
14、（1） ；
（2） ；
（3） 。
五、计算题（本题共4小题，15题6分，16题11分，17、18题各12分，只写最后答案不给分，有数值计算的题，答案中必须明确写出数值和单位）
15、解：
16、解：
17、（1）（ ）
（2）解：
18、解：
A. a和b之间的势能先增大，后减小
B. a和b的总动能先增大，后减小
C. 两分子相距r0时， a和b的加速度均不为零
D. 两分子相距r0时， a和b之间的势能大于零
查看习题详情和答案>>
当两分子间距为r0时，它们之间的引力和斥力相等。关于分子之间的相互作用，下列说法正确的是
- A.当两个分子间的距离小于r0时，分子间只存在斥力
- B.当两个分子间的距离大于r0时，分子间只存在引力
- C.两个分子间的距离由较远逐渐减小到r= r0的过程中，分子间相互作用力先增大后减小，表现为引力
- D.两个分子间的距离由r= r0开始减小的过程中，分子间相互作用力一直增大，表现为斥力
- E.两个分子间的距离等于r0时，分子势能最小
第十部分 磁场
第一讲 基本知识介绍
《磁场》部分在奥赛考刚中的考点很少，和高考要求的区别不是很大，只是在两处有深化：a、电流的磁场引进定量计算；b、对带电粒子在复合场中的运动进行了更深入的分析。
一、磁场与安培力
1、磁场
a、永磁体、电流磁场→磁现象的电本质
b、磁感强度、磁通量
c、稳恒电流的磁场
*毕奥-萨伐尔定律（Biot-Savart law）：对于电流强度为I 、长度为dI的导体元段，在距离为r的点激发的“元磁感应强度”为dB 。矢量式d
= k
，（d
表示导体元段的方向沿电流的方向、
为导体元段到考查点的方向矢量）；或用大小关系式dB = k
结合安培定则寻求方向亦可。其中 k = 1.0×10?7N/A2 。应用毕萨定律再结合矢量叠加原理，可以求解任何形状导线在任何位置激发的磁感强度。
毕萨定律应用在“无限长”直导线的结论：B = 2k
；
*毕萨定律应用在环形电流垂直中心轴线上的结论：B = 2πkI
；
*毕萨定律应用在“无限长”螺线管内部的结论：B = 2πknI 。其中n为单位长度螺线管的匝数。
2、安培力
a、对直导体，矢量式为 
= I
；或表达为大小关系式 F = BILsinθ再结合“左手定则”解决方向问题（θ为B与L的夹角）。
b、弯曲导体的安培力
⑴整体合力
折线导体所受安培力的合力等于连接始末端连线导体（电流不变）的的安培力。
证明：参照图9-1，令MN段导体的安培力F1与NO段导体的安培力F2的合力为F，则F的大小为
F = 
= BI
= BI
关于F的方向，由于ΔFF2P∽ΔMNO，可以证明图9-1中的两个灰色三角形相似，这也就证明了F是垂直MO的，再由于ΔPMO是等腰三角形（这个证明很容易），故F在MO上的垂足就是MO的中点了。
证毕。
由于连续弯曲的导体可以看成是无穷多元段直线导体的折合，所以，关于折线导体整体合力的结论也适用于弯曲导体。（说明：这个结论只适用于匀强磁场。）
⑵导体的内张力
弯曲导体在平衡或加速的情形下，均会出现内张力，具体分析时，可将导体在被考查点切断，再将被切断的某一部分隔离，列平衡方程或动力学方程求解。
c、匀强磁场对线圈的转矩
如图9-2所示，当一个矩形线圈（线圈面积为S、通以恒定电流I）放入匀强磁场中，且磁场B的方向平行线圈平面时，线圈受安培力将转动（并自动选择垂直B的中心轴OO′，因为质心无加速度），此瞬时的力矩为
M = BIS
几种情形的讨论——
⑴增加匝数至N ，则 M = NBIS ；
⑵转轴平移，结论不变（证明从略）；
⑶线圈形状改变，结论不变（证明从略）；
*⑷磁场平行线圈平面相对原磁场方向旋转α角，则M = BIScosα ，如图9-3；
证明：当α = 90°时，显然M = 0 ，而磁场是可以分解的，只有垂直转轴的的分量Bcosα才能产生力矩…
⑸磁场B垂直OO′轴相对线圈平面旋转β角，则M = BIScosβ ，如图9-4。
证明：当β = 90°时，显然M = 0 ，而磁场是可以分解的，只有平行线圈平面的的分量Bcosβ才能产生力矩…
说明：在默认的情况下，讨论线圈的转矩时，认为线圈的转轴垂直磁场。如果没有人为设定，而是让安培力自行选定转轴，这时的力矩称为力偶矩。
二、洛仑兹力
1、概念与规律
a、
= q
，或展开为f = qvBsinθ再结合左、右手定则确定方向（其中θ为
与
的夹角）。安培力是大量带电粒子所受洛仑兹力的宏观体现。
b、能量性质
由于
总垂直
与
确定的平面，故
总垂直
，只能起到改变速度方向的作用。结论：洛仑兹力可对带电粒子形成冲量，却不可能做功。或：洛仑兹力可使带电粒子的动量发生改变却不能使其动能发生改变。
问题：安培力可以做功，为什么洛仑兹力不能做功？
解说：应该注意“安培力是大量带电粒子所受洛仑兹力的宏观体现”这句话的确切含义——“宏观体现”和“完全相等”是有区别的。我们可以分两种情形看这个问题：（1）导体静止时，所有粒子的洛仑兹力的合力等于安培力（这个证明从略）；（2）导体运动时，粒子参与的是沿导体棒的运动v1和导体运动v2的合运动，其合速度为v ，这时的洛仑兹力f垂直v而安培力垂直导体棒，它们是不可能相等的，只能说安培力是洛仑兹力的分力f1 = qv1B的合力（见图9-5）。
很显然，f1的合力（安培力）做正功，而f不做功（或者说f1的正功和f2的负功的代数和为零）。（事实上，由于电子定向移动速率v1在10?5m/s数量级，而v2一般都在10?2m/s数量级以上，致使f1只是f的一个极小分量。）
☆如果从能量的角度看这个问题，当导体棒放在光滑的导轨上时（参看图9-6），导体棒必获得动能，这个动能是怎么转化来的呢？
若先将导体棒卡住，回路中形成稳恒的电流，电流的功转化为回路的焦耳热。而将导体棒释放后，导体棒受安培力加速，将形成感应电动势（反电动势）。动力学分析可知，导体棒的最后稳定状态是匀速运动（感应电动势等于电源电动势，回路电流为零）。由于达到稳定速度前的回路电流是逐渐减小的，故在相同时间内发的焦耳热将比导体棒被卡住时少。所以，导体棒动能的增加是以回路焦耳热的减少为代价的。
2、仅受洛仑兹力的带电粒子运动
a、
⊥
时，匀速圆周运动，半径r = 
，周期T = 
b、
与
成一般夹角θ时，做等螺距螺旋运动，半径r = 
，螺距d = 
这个结论的证明一般是将
分解…（过程从略）。
☆但也有一个问题，如果将
分解（成垂直速度分量B2和平行速度分量B1 ，如图9-7所示），粒子的运动情形似乎就不一样了——在垂直B2的平面内做圆周运动？
其实，在图9-7中，B1平行v只是一种暂时的现象，一旦受B2的洛仑兹力作用，v改变方向后就不再平行B1了。当B1施加了洛仑兹力后，粒子的“圆周运动”就无法达成了。（而在分解v的处理中，这种局面是不会出现的。）
3、磁聚焦
a、结构：见图9-8，K和G分别为阴极和控制极，A为阳极加共轴限制膜片，螺线管提供匀强磁场。
b、原理：由于控制极和共轴膜片的存在，电子进磁场的发散角极小，即速度和磁场的夹角θ极小，各粒子做螺旋运动时可以认为螺距彼此相等（半径可以不等），故所有粒子会“聚焦”在荧光屏上的P点。
4、回旋加速器
a、结构&原理（注意加速时间应忽略）
b、磁场与交变电场频率的关系
因回旋周期T和交变电场周期T′必相等，故 
=
c、最大速度 vmax = 
= 2πRf
5、质谱仪
速度选择器&粒子圆周运动，和高考要求相同。
第二讲 典型例题解析
一、磁场与安培力的计算
【例题1】两根无限长的平行直导线a、b相距40cm，通过电流的大小都是3.0A，方向相反。试求位于两根导线之间且在两导线所在平面内的、与a导线相距10cm的P点的磁感强度。
【解说】这是一个关于毕萨定律的简单应用。解题过程从略。
【答案】大小为8.0×10?6T ，方向在图9-9中垂直纸面向外。
【例题2】半径为R ，通有电流I的圆形线圈，放在磁感强度大小为B 、方向垂直线圈平面的匀强磁场中，求由于安培力而引起的线圈内张力。
【解说】本题有两种解法。
方法一：隔离一小段弧，对应圆心角θ ，则弧长L = θR 。因为θ →
查看习题详情和答案>>[物理——选修3-3]
（1）根据分子动理论，分子间同时存在着相互作用的引力和斥力，以及具有分子势能。当分子间距离减小时，下列说法正确的是：（ ）
A.分子间引力一定增大 B.分子间斥力一定减小
C.分子势能一定增大 D.引力和斥力的合力一定增大
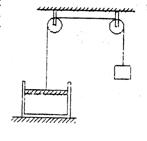
（2）如图所示的气缸中封闭着一定质量的理想气体，一重物用绳索经滑轮与缸中活塞相连接，活塞和气缸都导热，活塞与气缸间无摩擦，原先重物和活塞均处于平衡状态，因温度下降使气缸中气体做等压变化，下列说法正确的是（ ）
A.重物上升，气体放出热量
B.重物上升，气体吸收热量
C.重物下降，气体放出热量
D.重物下降，气体吸收热量
(1)下列说法中正确的是 。
A．布朗运动就是液体分子的热运动
B．分子间距离等于分子间平衡距离时，分子势能最小
C．能量耗散是从能量转化的角度反映出自然界中的宏观过程具有的方向性
D．一定质量的理想气体在温度不变的条件下，压强增大，则气体对外界做功
E．当液晶中电场强度不同时，它对不同颜色的光吸收强度不同，就能显示各种颜色
(2)在“用油膜法估测分子直径”的实验中，有下列操作步骤：
A．用滴管将浓度为0．05％的油酸酒精溶液逐摘滴入量筒中，记下滴入1mL的油酸酒精溶
液的滴数N
B．将痱子粉末均匀地撒在浅盘内的水面上，用滴管吸取浓度为0．05％的油酸酒精溶液，逐滴向水面上滴入，直到油酸薄膜表面积足够大，且不与器壁接触为止，记下滴入的滴数n
C．
D．将画有油酸薄膜轮廓的玻璃板放在坐标纸上，以坐标纸上边长lcm的正方形为单位，计算出轮廓内正方形的个数m
E．用上述测量的物理量可以估算出单个油酸分子的直径d。
请你补充实验步骤C的内容及写出实验步骤E中d的计算表达式。
(3)一定质量的理想气体由状态A经过程I变至状态B时，从外界吸收热量420J，同时膨胀对
外做功300J。当气体从状态B经过程Ⅱ回到状态A时，外界压缩气体做功200J，求此过
程中气体吸收或放出的热量。
查看习题详情和答案>>