摘要:故2.5 m/s<v0<5 m/s(2)由L=v01t 得t=4×10-2 s
网址:http://m.1010jiajiao.com/timu_id_402886[举报]
如图甲所示,两个平行金属板P、Q竖直放置,两板间加上如图乙所示的电压,t=0时,Q板比P板电势高5 V,此时在两板的正中央M点有一个电子,速度为零,电子在电场力作用下运动,使得电子的位置和速度随时间变化。假设电子始终未与两板相碰。在0<t<8×10-10 s的时间内,这个电子处于M点的右侧,速度方向向左且大小逐渐减小的时间是( )
A.0<t<2×10-10 s
B.2×10-10 s<t<4×10-10 s
C.4×10-10 s<t<6×10-10 s
D.6×10-10 s<t<8×10-10 s

如图二所示,一阶梯高宽都为0.4m,一球以水平速度v飞出,欲打在第四级台阶上,则v的取值范围是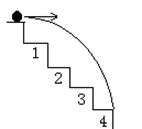
A. m/s<v≤2 m/s<v≤2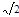 m/s m/s |
B.2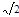 m/s <v≤3.5 m/s m/s <v≤3.5 m/s |
C.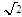 m/s <v≤ m/s <v≤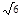 m/s m/s |
D.2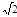 m/s <v≤ m/s <v≤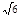 m/s m/s |
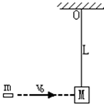 如图所示:质量为M=0.6kg的小沙箱,用长为L=1.60m的细线悬于空中某点,现用玩具手枪以v0=10m/s速度从左向右向沙箱发射质量m=0.2kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹与沙箱迎面飞来,射入沙箱并留在其中,不计空气阻力,细线能承受的拉力足够大,子弹与沙箱的作用时间极短,取g=10m/s2,求解下列问题:
如图所示:质量为M=0.6kg的小沙箱,用长为L=1.60m的细线悬于空中某点,现用玩具手枪以v0=10m/s速度从左向右向沙箱发射质量m=0.2kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹与沙箱迎面飞来,射入沙箱并留在其中,不计空气阻力,细线能承受的拉力足够大,子弹与沙箱的作用时间极短,取g=10m/s2,求解下列问题:(1)第一颗子弹射入沙箱时,沙箱的速度是多大?此后沙箱能否作完整的圆周运动,试计算说明.
(2)对于第二颗子弹打入沙箱时沙箱速度的求解,有位同学作了如下的解法:设第二颗子弹打入沙箱后沙厢的速度为v2,则由动量守恒定律:2mv0=(M+2m)v2,故v2=
| 2mv0 |
| M+2m |
| 2×0.2×10 |
| 0.6+2×0.2 |
(3)第三颗子弹打入沙箱时,沙箱的速度为多少?
(4)停止射击后,要使沙箱静止在最低点,射入沙箱的子弹数目为n,则n应取
C
C
A.只能n=2
B.n为任意奇数
C.n为任意偶数
D.不论n为多少,沙箱均不能静止在最低点.
 =1.0×10-2 kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿
=1.0×10-2 kg的绝缘物块.物块与水平面间的动摩擦因数μ=0.20,沿