网址:http://m.1010jiajiao.com/timu_id_40133[举报]
一.选择题(本大题共12小题,每小题5分,共60分.)
D C B B C D C A C C A A
二.填空题(本大题共4小题,每小题4分,共16分.)
(13) (14)
(14) (15)―1 (16)
(15)―1 (16)
三.解答题
(17)(本小题满分12分)
解:(Ⅰ):

 . 3分
. 3分
依题意, 的周期
的周期 ,且
,且 ,∴
,∴  .∴
.∴ .
.
∴  . 5分
. 5分
∵ 
 [0,
[0, ], ∴
], ∴  ≤
≤ ≤
≤ ,∴
,∴  ≤
≤ ≤1,
≤1,
∴  的最小值为
的最小值为  ,即
,即  ∴
∴
 .
.
∴  . 7分
. 7分
(Ⅱ)∵  =2
=2
 , ∴
, ∴  .
.
又 ∵ ∠ ∈(0,
∈(0, ), ∴ ∠
), ∴ ∠ =
= . 9分
. 9分
在 △ABC中,∵
△ABC中,∵  ,
, ,
,
∴  ,
, .解得
.解得 

 .
.
又 ∵ 0 , ∴
, ∴ 
 . 12分
. 12分
 (18)(本小题满分12分)
(18)(本小题满分12分)
解:以A点为原点,AB为 轴,AD为
轴,AD为 轴,AD
轴,AD
为 轴的空间直角坐标系,如图所示.则依题意可知相
轴的空间直角坐标系,如图所示.则依题意可知相
关各点的坐标分别是A(0,0,0),B( ,0,0),
,0,0),
C( ,1,0),D(0,1,0),S(0,0,1),
,1,0),D(0,1,0),S(0,0,1),
∴ M( ,1,0),N(
,1,0),N( ,
, ,
, ). 2分
). 2分
∴  (0,
(0, ,
, ),
), (
( ,0,0),
,0,0), (
( ,
, ,
, ). 4分
). 4分
∴  ,
, .∴
.∴  ,
, .
.
∴ MN ⊥平面ABN. 6分
(Ⅱ)设平面NBC的法向量为 (
( ,
, ,
, ),则
),则 ,
, .且又易知
.且又易知  ,
, .
.
∴  即
即  ∴
∴ 
令 ,则
,则 (
( ,0,
,0, ). 9分
). 9分
显然, (0,
(0, ,
, )就是平面ABN的法向量.
)就是平面ABN的法向量.
∴  .
.
∴ 二面角 的余弦值是
的余弦值是 . 12分
. 12分
(19)(本小题满分12分)
解:(Ⅰ)由题意得

 (
( ); 3分
); 3分
同理可得 (
( );
);
 (
( ). 5分
). 5分
(Ⅱ) . 8分
. 8分
(Ⅲ)由上问知
 ,即
,即 是关于
是关于 的三次函数,设
的三次函数,设
 ,则
,则 .
.
令 ,解得
,解得  或
或  (不合题意,舍去).
(不合题意,舍去).
显然当  时,
时, ;当
;当  时,
时, .
.
∴ 当年产量
 时,随机变量
时,随机变量
 的期望
的期望  取得最大值. 12分
取得最大值. 12分
(20)(本小题满分12分)
解:(Ⅰ)设 (
( ,
, )是函数
)是函数  的图象上任意一点,则容易求得
的图象上任意一点,则容易求得 点关于直线
点关于直线  的对称点为
的对称点为 (
( ,
, ),依题意点
),依题意点 (
( ,
, )在
)在 的图象上,
的图象上,
∴
 . ∴
. ∴  . 2分
. 2分
∴
 .
.
∵  是
是  的一个极值点,∴
的一个极值点,∴  ,解得
,解得  .
.
∴ 函数  的表达式是
的表达式是  (
( ). 4分
). 4分
∴
 .
.
∵ 函数  的定义域为(
的定义域为( ), ∴
), ∴  只有
只有 一个极值点,且显然当
一个极值点,且显然当
 时,
时, ;当
;当 时,
时, .
.
∴ 函数  的单调递增区间是
的单调递增区间是 ;单调递减区间是
;单调递减区间是 . 6分
. 6分
(Ⅱ)由 
 ,
,
得
 ,∴
,∴  . 9分
. 9分
∴  在
在 时恒成立.
时恒成立.
∴
只需求出  在
在  时的最大值和
时的最大值和
 在
在
时的最小值,即可求得
 的取值范围.
的取值范围.
∵  (当
(当 时);
时);
 (当
(当 时).
时).
∴
 的取值范围是
的取值范围是  .
12分
.
12分
 (21)(本小题满分12分)
(21)(本小题满分12分)
解:(Ⅰ)∵  ,
,
∴ .
.
设O关于直线  的
的
对称点为 的横坐标为
的横坐标为  .
.
又易知直线 解得线段
解得线段 的中点坐标
的中点坐标
为(1,-3).∴ .
.
∴ 椭圆方程为  . 5分
. 5分
(Ⅱ)显然直线AN存在斜率,设直线AN的方程为  ,代入
,代入  并整理得:
并整理得: .
.
设点 ,
, ,则
,则 .
.
由韦达定理得  ,
, . 8分
. 8分
∵ 直线ME方程为  ,令
,令 ,得直线ME与x轴的交点的横坐标
,得直线ME与x轴的交点的横坐标  .
.
将 ,
, 代入,并整理得
代入,并整理得  . 10分
. 10分
再将韦达定理的结果代入,并整理可得 .
.
∴ 直线ME与 轴相交于定点(
轴相交于定点( ,0). 12分
,0). 12分
(22)(本小题满分14分)
证明:(Ⅰ)∵
 ,
, ,且
,且  (
( ,
, N?),
N?),
∴
 . 2分
. 2分
将
 去分母,并整理得
去分母,并整理得  . 5分
. 5分
∴
 ,
, ,……,
,……, ,
,
将这 个同向不等式相加,得
个同向不等式相加,得  ,∴
,∴  . 7分
. 7分
(Ⅱ)∵
 ,∴
,∴  . 9分
. 9分
∴
 .即
.即  . 11分
. 11分
∴  ,即
,即
 . 14分
. 14分
某企业准备投产一种新产品,经测算,已知每年生产![]() 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为![]() 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
| 市场情况 | 概率 | 价格p与产量x的函数关系式 |
| 好 | 0.3 |
|
| 中 | 0.5 |
|
| 差 | 0.2 |
|
设L1、L2、L3分别表示市场情况好、中、差时的利润,随机变量ξx表示当年产量为x而市场情况不确定时的利润.
(1)分别求利润L1、L2、L3与年产量x之间的函数关系式;
(2)当产量x确定时,求随机变量ξx的期望Eξx;
(3)求年产量x为何值时,随机变量ξx的期望Eξx取得最大值(不需求最大值).
查看习题详情和答案>>某企业准备投产一种新产品,经测算,已知每年生产
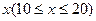 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为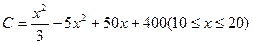 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.| 市场情况 | 概率 | 价格p与产量x的函数关系式 |
| 好 | 0.3 | 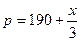 |
| 中 | 0.5 | 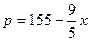 |
| 差 | 0.2 | 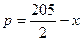 |
(1)分别求利润L1、L2、L3与年产量x之间的函数关系式;
(2)当产量x确定时,求随机变量ξx的期望Eξx;
(3)求年产量x为何值时,随机变量ξx的期望Eξx取得最大值(不需求最大值).
(08年威海市模拟理)(12分)某企业准备投产一种新产品,经测算,已知每年生产![]() 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为![]() 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
市场情况 | 概率 | 价格p与产量x的函数关系式 |
好 | 0.3 |
|
中 | 0.5 |
|
差 | 0.2 |
|
设L1、L2、L3分别表示市场情况好、中、差时的利润,随机变量ξx表示当年产量为x而市场情况不确定时的利润.
(1)分别求利润L1、L2、L3与年产量x之间的函数关系式;
(2)当产量x确定时,求随机变量ξx的期望Eξx;
(3)求年产量x为何值时,随机变量ξx的期望Eξx取得最大值(不需求最大值) 查看习题详情和答案>>