网址：http://m.1010jiajiao.com/timu_id_393774[举报]
1．A 2．D 3．B 4．AC 5．B 6．B 7．B 8．AC 9．ABD 10．BD
11．⑴①③②④ (2分)
⑵D (2分)
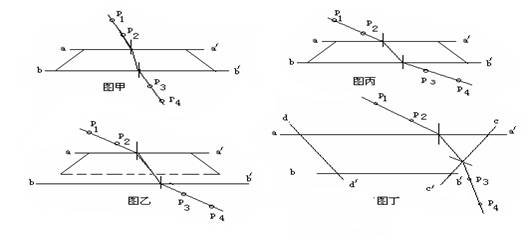
⑶
是n个点对应的圆心角，t是打点计时器的打点时间间隔
(2分)
⑷没有影响 (1分)
12．⑴乙同学的猜想是对的，当新弹簧所受拉力为F时，其中A弹簧的伸长量
，B弹簧的伸长量
，而
，可得
(3分)
⑵铁架台，刻度尺 (2分)
⑶①将新弹簧悬挂在铁架台上，用刻度尺测出弹簧的长度
②在弹簧下端挂上n个钩码，测出此时弹簧的长度
③将测量结果代入
得到
的值
④改变n的值，多测几次，取的平均值代入进行验证 (3分)
13．解：设轨道ab与水平面间的夹角为θ，由几何关系可知：
轨道ab的长度
(3分)
由牛顿第二定律可得，小球下滑的加速度
(2分)
由运动学公式得 
(2分)
联立以上各式解得 
(2分)
14．解：⑴设中央恒星O的质量为M，A行星的质量为m，则由万有引力定律和牛顿第二定律得
(3分)
解得 
(1分)
⑵由题意可知：A、B相距最近时，B对A的影响最大，且每隔
时间相距最近，设B行星的周期为
，则有 
(1分)
解得 
(1分)
设B行星的运行轨道半径为
，根据开普勒第三定律有 
(2分)
解得 
(1分)
15．解：⑴被困人员在水平方向上做匀速直线运动，在竖直方向上被困人员的位移
，由此可知，被困人员在竖直方向上做初速度为零、加速度
的匀加速直线运动 (2分)
由牛顿第二定律可得 
(1分 )
解得悬索的拉力 
(1分)
⑵被困人员5s末在竖直方向上的速度为 
(1分)
合速度 
(1分)
竖直方向的位移 
，水平方向的位移
，合位移
(2分)
⑶
时悬索的长度
，旋转半径
，由
解得 
(2分)
此时被困人员B的受力情况如图所示，由图可知
解得 
(2分)
16．⑴米袋在AB上加速时的加速度
(1分)
米袋的速度达到
时，滑行的距离
，因此米袋在到达B点之前就有了与传送带相同的速度 (2分)
设米袋在CD上运动的加速度大小为a，由牛顿第二定律得
(1分)
代入数据得 
(1分)
所以能滑上的最大距离 
(1分)
⑵设CD部分运转速度为
时米袋恰能到达D点(即米袋到达D点时速度恰好为零)，则米袋速度减为之前的加速度为
(1分)
米袋速度小于至减为零前的加速度为
(1分)
由
(2分)
解得 
，即要把米袋送到D点，CD部分的速度
(1分)
米袋恰能运到D点所用时间最长为
(1分)
若CD部分传送带的速度较大，使米袋沿CD上滑时所受摩擦力一直沿皮带向上，则所用时间最短，此种情况米袋加速度一直为
。
由
(1分)
所以，所求的时间t的范围为 
(1分)
（1）同学们通过查阅资料知道将锌、铜两电极插入水果中，电动势大约会有1伏多一点。甲同学找来了一个土豆做实验，当用量程为0～3V、内阻约50kΩ的电压表测其两极时读数为0.96V，但当他将四个这样的水果电池串起来给标称值为“3V，0.5A”的小灯泡供电时，灯泡并不发光，检查灯泡、线路均无故障。据你猜想，出现这种现象的原因是：_______________________________________。（不要求写分析、推导过程）
（3）为了更准确测定一个“土豆电池”的电动势和内阻，实验室提供了以下一些器材可供选择：
A．电流表A1（量程为0～0 6A，内阻r1=1Ω）
B．灵敏电流表A2（量程为0～0.6mA，内阻r=800Ω）
C．灵敏电流表A3（量程为0～250μA，内阻未知）
D．滑动变阻器R（最大阻值约10Ω）
E．定值电阻R0（阻值2kΩ）
F．变阻箱R′（0～9999Ω）
G．开关S和导线若干
①为了能尽可能准确测定“土豆电池”的电动势和内阻，实验中除了带有锌、铜两电极的水果电池外，还应选择的器材是_____________（填器材前的字母代号）；
②利用①问中选择的器材，在方框中画出测量的电路图（图中要标明相关器材的字母代号）。
（14分）学过单摆的周期公式以后，物理兴趣小组的同学们对钟摆产生了兴趣，老师建议他们先研究用厚度和质量分布均匀的长木条（如一把米尺）做成的摆（这种摆被称为复摆），如图 所示。让其在竖直平面内做小角度摆动，C 点为重心，木条长为 L ，周期用 T 表示 。
甲同学猜想：复摆的周期应该与木条的质量有关。
乙同学猜想：复摆的摆长应该是悬点到重心的距离 L/2 。
丙同学猜想：复摆的摆长应该大于 L/2 。理由是：若 OC 段看成细线，线栓在C处，C点以下部分的重心离O点的距离显然大于L/2。
为了研究以上猜想是否正确，同学们进行了下面的实验探索：
（1） 把两个相同的长木条完全重叠在一起，用透明胶（质量不计）粘好，测量其摆动周期，发现与单个长木条摆动时的周期相同，重做多次仍有这样的特点。则证明了甲同学的猜想是 的（选填“正确”或“错误”） 。
（2） 用 To 表示木条长为 L 的复摆看成摆长为 L/2 单摆的周期计算值（To = 2π
），用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表：
由上表可知，复摆的等效摆长 L/2 （选填“大于”、“小于”或“等于”） 。
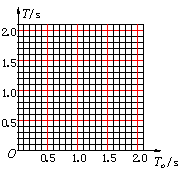
（3） 为了进一步定量研究，同学们用描点作图法对数据进行处理，所选坐标
如图 13 所示。请在坐标纸上作出 T – To图线，并根据图象中反映出的规律求出
/
= （结果保留三位有效数字，其中 L等 是木条长为L时的等效摆长。T = 2π
） 。
 |
 |
| 板长L（cm） | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值To /（s） | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/（s） | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
（14分）学过单摆的周期公式以后，物理兴趣小组的同学们对钟摆产生了兴趣，老师建议他们
先研究用厚度和质量分布均匀的长木条（如一把米尺）做成的摆（这种摆被称为复摆），如图
所示。让其在竖直平面内做小角度摆动，C 点为重心，木条长为 L ，周期用 T 表示 。
甲同学猜想：复摆的周期应该与木条的质量有关。
乙同学猜想：复摆的摆长应该是悬点到重心的距离 L/2 。
丙同学猜想：复摆的摆长应该大于 L/2 。理由是：若 OC 段看成细线，线栓在C处，
C点以下部分的重心离O点的距离显然大于L/2。
为了研究以上猜想是否正确，同学们进行了下面的实验探索：
（1） 把两个相同的长木条完全重叠在一起，用透明胶（质量不计）粘好，测量其摆动周期，发现与单个长木条摆动时的周期相同，重做多次仍有这样的特点。则证明了甲同学的猜想是 的（选填“正确”或“错误”） 。
（2） 用 To 表示木条长为 L 的复摆看成摆长为 L/2 单摆的周期计算值（To = 2π
），用 T 表示木条长为 L 复摆的实际周期测量值。计算与测量的数据如下表：
| 板长L（cm） | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值To /（s） | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/（s） | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
由上表可知，复摆的等效摆长 L/2 （选填“大于”、“小于”或“等于”） 。
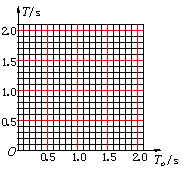
（3） 为了进一步定量研究，同学们用描点作图法对数据进行处理，所选坐标
如图 13 所示。请在坐标纸上作出 T – To图线，并根据图象中反映出的规律求出
/
= （结果保留三位有效数字，其中 L等 是木条长为L时的等效摆长。T = 2π
） 。
 |
 |
查看习题详情和答案>>
