摘要：分比定理:

网址：http://m.1010jiajiao.com/timu_id_392687[举报]

定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：

+y2=1．
（1）若椭圆C2：

=1，判断C₂与C₁是否相似？如果相似，求出C₂与C₁的相似比；如果不相似，请说明理由；
（2）写出与椭圆C₁相似且短半轴长为b的椭圆C_b的方程；若在椭圆C_b上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
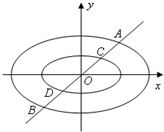
（3）如图：直线y=x与两个“相似椭圆”M：

=λ2(a＞b＞0，0＜λ＜1)分别交于点A，B和点C，D，试在椭圆M和椭圆M_λ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）查看习题详情和答案>>

定义：离心率e=

的椭圆为“黄金椭圆”，已知椭圆E：

=1(a＞b＞0)的两个焦点分别为F₁（-c，0）、F₂（c，0）（c＞0），P为椭圆E上的任意一点．
（1）试证：若a，b，c不是等比数列，则E一定不是“黄金椭圆”；
（2）设E为“黄金椭圆”，问：是否存在过点F₂、P的直线l，使l与y轴的交点R满足

？若存在，求直线l的斜率k；若不存在，请说明理由；
（3）设E为“黄金椭圆”，点M是△PF₁F₂的内心，连接PM并延长交F₁F₂于N，求

查看习题详情和答案>>

：. 甲、乙两个水平相当的选手在决赛中相遇，决定采用五局三胜制，当比赛进行到甲对乙的比分为2︰1时，因故比赛停止，乙要求比赛奖金甲与乙按2︰1的比例分发；你认为这种分发方案合理吗？请说明理由。若不合理，应怎样分发？

查看习题详情和答案>>

定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆 $数学公式$ ．
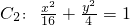（1）若椭圆 $数学公式$ ，判断C₂与C₁是否相似？如果相似，求出C₂与C₁的相似比；如果不相似，请说明理由；
（2）写出与椭圆C₁相似且短半轴长为b的椭圆C_b的方程；若在椭圆C_b上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
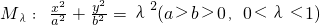（3）如图：直线y=x与两个“相似椭圆” $数学公式$ 和 $数学公式$ 分别交于点A，B和点C，D，试在椭圆M和椭圆M_λ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）

查看习题详情和答案>>

定义：将一个数列中部分项按原来的先后次序排列所成的一个新数列称为原数列的一个子数列．
已知无穷等比数列{a_n}的首项、公比均为 $数学公式$ ．
（1）试求无穷等比子数列{a_3k-1}（k∈N^*）各项的和；
（2）是否存在数列{a_n}的一个无穷等比子数列，使得它各项的和为 $数学公式$ ？若存在，求出满足条件的子数列的通项公式；若不存在，请说明理由；
（3）试设计一个数学问题，研究：是否存在数列{a_n}的两个不同的无穷等比子数列，使得其各项和之间满足某种关系．请写出你的问题以及问题的研究过程和研究结论．

查看习题详情和答案>>