摘要：其中.半径是.圆心坐标是
网址：http://m.1010jiajiao.com/timu_id_392622[举报]
在平面斜坐标系xOy中，z：xOy＝120°，平面上任一点M关于斜坐标系的斜坐标是这样定义的：
(其中e1、e2分别为与x轴、y轴同方向的单位向量)，则P点斜坐标为(x，y)．那么以O为圆心，2为半径的圆在斜坐标系xOy少中的方程为
[ ]
A．x2＋y2＋xy＝4
B．x2＋y2＝4
C．x2＋y2－xy＝4
D．以上都不是
如图所示，直角坐标系xOy建立在湖泊的某一恰当位置，现准备在湖泊的一侧修建一条观光大道，它的前一段MD是以O为圆心，OD为半径的圆弧，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
），x∈[4，8]时的图象，图象的最高点为B(5，
)
（Ⅰ）求函数y=sin（ωx+φ）的解析式；
（Ⅱ）若在湖泊内修建如图所示的矩形水上乐园OEPF，其中折线FPE为水上赛艇线路，问点P落在圆弧MD上何处时赛艇线路最长？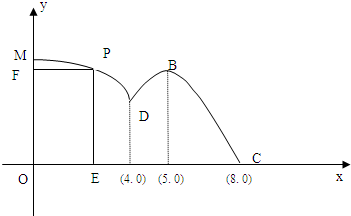
查看习题详情和答案>>
| π |
| 2 |
| 8 |
| 3 |
（Ⅰ）求函数y=sin（ωx+φ）的解析式；
（Ⅱ）若在湖泊内修建如图所示的矩形水上乐园OEPF，其中折线FPE为水上赛艇线路，问点P落在圆弧MD上何处时赛艇线路最长？
查看习题详情和答案>>
在解析几何里，圆心在点（x0，y0），半径是r（r＞0）的圆的标准方程是（x-x0）2+（y-y0）2=r2．类比圆的标准方程，研究对称轴平行于坐标轴的椭圆的标准方程，可以得出的正确结论是：“设椭圆的中心在点（x0，y0），焦点在直线y=y0上，长半轴长为a，短半轴长为b（a＞b＞0），其标准方程为
+
=1
+
=1．
查看习题详情和答案>>
| (x-x0)2 |
| a2 |
| (y-y0)2 |
| b2 |
| (x-x0)2 |
| a2 |
| (y-y0)2 |
| b2 |
），x∈[4，8]时的图象，图象的最高点为
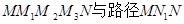都是M到N的“L路径”。某地有三个新建的居民区，分别位于平面xOy内三点
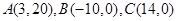处。现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心。