摘要:圆的一般方程是:
网址:http://m.1010jiajiao.com/timu_id_392621[举报]
在平面直角坐标系中,已知焦距为4的椭圆 的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为 .
.
(1)求椭圆C的方程;
(2)设Q(t,m)是直线x=9上的点,直线QA、QB与椭圆C分别交于点M、N,求证:直线MN
必过x轴上的一定点,并求出此定点的坐标;
(3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线y2=2px(p>0)写出一个更一般的结论,并加以证明.
查看习题详情和答案>>
在平面直角坐标系中,已知焦距为4的椭圆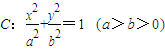 的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为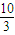 .
.
(1)求椭圆C的方程;
(2)设Q(t,m)是直线x=9上的点,直线QA、QB与椭圆C分别交于点M、N,求证:直线MN
必过x轴上的一定点,并求出此定点的坐标;
(3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线y2=2px(p>0)写出一个更一般的结论,并加以证明.
查看习题详情和答案>>
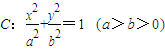 的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为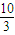 .
.(1)求椭圆C的方程;
(2)设Q(t,m)是直线x=9上的点,直线QA、QB与椭圆C分别交于点M、N,求证:直线MN
必过x轴上的一定点,并求出此定点的坐标;
(3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线y2=2px(p>0)写出一个更一般的结论,并加以证明.
查看习题详情和答案>>
请考生注意:重点高中学生只做(1)、(2)两问,一般高中学生只做(1)、(3)两问.
已知P是圆F1:(x+1)2+y2=16上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且
=
(
+
),|
+
|=|
-
|.
(1)求点M的轨迹C的方程;
(2)斜率为k的直线l与曲线C交于P、Q两点,若
•
=0(O为坐标原点).试求直线l在y轴上截距的取值范围;
(3)是否存在斜率为
的直线l与曲线C交于P、Q两点,使得
•
=0(O为坐标原点),若存在求出直线l的方程,否则说明理由.
查看习题详情和答案>>
已知P是圆F1:(x+1)2+y2=16上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且
| MN |
| 1 |
| 2 |
| MF2 |
| MP |
| NM |
| F2P |
| NM |
| F2P |
(1)求点M的轨迹C的方程;
(2)斜率为k的直线l与曲线C交于P、Q两点,若
| OP |
| OQ |
(3)是否存在斜率为
| 1 |
| 2 |
| OP |
| OQ |
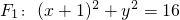 上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且
上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且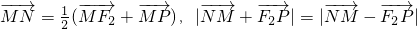 .
. (O为坐标原点).试求直线l在y轴上截距的取值范围;
(O为坐标原点).试求直线l在y轴上截距的取值范围; 的直线l与曲线C交于P、Q两点,使得
的直线l与曲线C交于P、Q两点,使得