网址:http://m.1010jiajiao.com/timu_id_386733[举报]
一、二、选择题
题号
1
2
3
4
5
6
7
8
9
答案
C
B
C
A
D
CD
BC
AC
ABD
 三、简答题
三、简答题
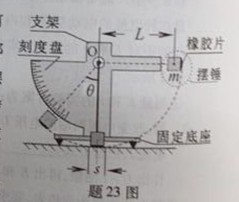
10.每小题2分,计8分。
(1)C;
(2) ;
;
(3)m<<M;
(4)如图所示。
11.(3)4分,其余每小题2分,计10分。
(1)保护电源、电表,防止短路;
(2)作图;
(3)1.5, 1.0 (3.0不正确)
 (4)30,5
(4)30,5
(1)CD
(2)AB
(3)1.2×10-5Pa;内能增加了1.8×105J
12B.(每小题4分,计12分)
(1)①1:3 ②4:1
(2)CD
(3)(3)发生;450
(1)C
(2)B
(3)2
 四、全题共计47分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
四、全题共计47分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
13.解:(1)在D点,速度为vD,
mg = mvD2/R
∴v=2m/s
由A运动到D点,机械能守恒
mg(h-2R)= mvD2/2
∴h=1m
(2)由A运动到C点,机械能守恒
mgh=mvC2/2
在C点,由向心力公式,得
FN-mg=mvC2/R
∴FN=12N
(3)设撞到斜面上E点离B点的距离为x,飞行时间为t,由位移公式,得
Rsin530+xcos530 = vDt
R+Rcos530-xsin530 = gt2/2
由上面两式,得
t = s
评分:(1)(2)各4分,(3)中列式4分,结果4分。
14.解:(1)粒子进入磁场后做圆周运动的轨道半径为r

∴
(2)O、P连线与x轴之间的夹角为45°,由运动的对称性,粒子经两个四分之一圆弧到达P点,设圆周运动周期为T0,由T0= ,得
,得
T0= ∴T= =
∴T= =
 (3)设两段圆弧的圆心OO的连线与y轴夹角为θ,P点的纵坐标为y,圆心O到y轴之间的距离为x,则由几何关系,得
(3)设两段圆弧的圆心OO的连线与y轴夹角为θ,P点的纵坐标为y,圆心O到y轴之间的距离为x,则由几何关系,得
y=2r+2rcosθ
sinθ=
保证粒子在第一象限内运动,
x≥r
当θ=300时,y取最大,
ym=(2+)
评分标准:(1)4分(2)4分,(3中各式2分,计8分。
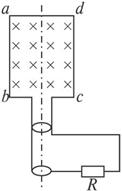
15.解:(1)拉力F作用过程中,在时间△t内,磁通量为△Φ,通过电阻R上电量q
 ,
,
 ,
,
 ,
,

(2)撤去F后金属棒滑行过程中动能转化为电能
∵
由能量守恒定律,得

∴
(3)匀速运动时最大拉力与安培力平衡

由图像面积,可得拉力做功为

由动能定理,得

电阻R上产生的热量( )
)

评分标准:(1)各式1分,计4分(2)各式2分,计6分,(3中各式2分,计6分。
(23分)如图为一传送装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带后,最后抛入固定于水平地面上的圆弧形槽内。已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m。圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°。当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内。当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求:

(1)传送带静止时,货物到达C点的速度大小和D点时的速度大小。
(2)求S1、S2的值应满足的关系。(sin53°= 0.8,cos53°= 0.6 )
查看习题详情和答案>>
(23分)如图为一传送装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带后,最后抛入固定于水平地面上的圆弧形槽内。已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m。圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°。当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内。当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求: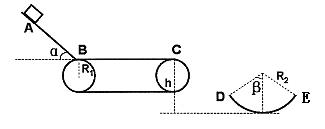
(1)传送带静止时,货物到达C点的速度大小和D点时的速度大小。
(2)求S1、S2的值应满足的关系。(sin53°= 0.8,cos53°= 0.6 )
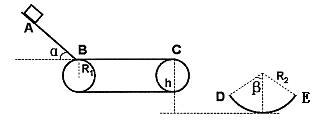
(1)传送带静止时,货物到达C点的速度大小和D点时的速度大小。
(2)求S1、S2的值应满足的关系。(sin53°= 0.8,cos53°= 0.6 )