网址:http://m.1010jiajiao.com/timu_id_37579[举报]
(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是![]() 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分![]() 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记![]() 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7[来源:Z#xx#k.Com] | 8 |
| 数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数 | 72 | 77 | 80[来源:学科网] | 84 | 88 | 90 | 93 | 95 |
根据上表数据可知,变量![]() 与
与![]() 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式:![]() ,其中
,其中 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(本小题满分12分)
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
|
组别 |
PM2.5(微克/立方米) |
频数(天) |
频率 |
|
第一组 |
(0,15] |
4 |
0.1 |
|
第二组 |
(15,30] |
12 |
0.3 |
|
第三组 |
(30,45] |
8 |
0.2 |
|
第四组 |
(45,60] |
8 |
0.2 |
|
第三组 |
(60,75] |
4 |
0.1 |
|
第四组 |
(75,90) |
4 |
0.1 |
(1)写出该样本的众数和中位数(不必写出计算过程);
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为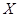 ,求
,求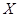 的分布列及数学期望
的分布列及数学期望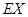 .
.
查看习题详情和答案>>
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7[来源:Z#xx#k.Com] |
8 |
|
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数 |
72 |
77 |
80[来源:] |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知,变量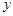 与
与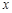 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出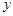 与
与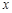 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: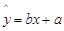 ,其中
,其中 ,
,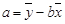 ;参考数据:
;参考数据: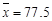 ,
,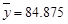 ,
, ,
,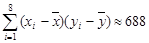 ,
, ,
,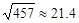 ,
,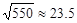 )
)
查看习题详情和答案>>