网址:http://m.1010jiajiao.com/timu_id_37260[举报]
一、选择题(本题共10小题,每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
A
A
D
B
A
C
B
二、填空题(本题共6小题,每小题5分,共30分)
11. 12.
12. 13.
13.
14. 15.
15. 16.
16.
三、解答题(本题有8小题,共80分)
17.(本题8分)
(1)原式
(2)解: 得:
得: ,
, ,
,
把 代入①得:
代入①得: ,
,
18.(本题8分)
(1)证明: ,
, ,
,
在 和
和 中
中


(2)答案不惟一,如: ,
, ,
, 等.
等.
19.(本题8分)
解:(1)方法一:列表得
A
B
C
D
 A
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
方法二:画树状图


(2)获奖励的概率: .
.
20.(本题8分)
(1)


(2) ,
, ,
, .
.
21.(本题10分)
解:(1)
 是
是 的切线,
的切线,
 ,
,
 ,
, .
.
(2) ,
, ,
, .
.
(3) ,
, ,
, ,
, ,
,
 ,
, .
.
22.(本题12分)
解:(1) ;40;
;40;
(2)人均进球数 .
.
(3)设参加训练前的人均进球数为 个,由题意得:
个,由题意得:
 ,解得:
,解得: .
.
答:参加训练前的人均进球数为4个.
23.(本题12分)
(1)


(2)由题意得: ,
,
 ,
, ,
, (m).
(m).
(3) ,
, ,
,
设 长为
长为 ,则
,则 ,解得:
,解得: (m),即
(m),即 (m).
(m).
同理 ,解得
,解得 (m),
(m), .
.
24.(本题14分)
解:(1)直线 的解析式为:
的解析式为: .
.
(2)方法一, ,
, ,
, ,
,
 ,
, ,
,
 是等边三角形,
是等边三角形, ,
,
 ,
, .
.
方法二,如图1,过 分别作
分别作 轴于
轴于 ,
, 轴于
轴于 ,
,
 可求得
可求得 ,
,
 ,
,

 ,
,
当点 与点
与点 重合时,
重合时,
 ,
,
 .
.
 ,
,

 .
.
(3)①当 时,见图2.
时,见图2.
设 交
交 于点
于点 ,
,
重叠部分为直角梯形 ,
,
作 于
于 .
.
 ,
, ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 随
随 的增大而增大,
的增大而增大,
 当
当 时,
时, .
.
②当 时,见图3.
时,见图3.
设 交
交 于点
于点 ,
,
交 于点
于点 ,
, 交
交 于点
于点 ,
,
重叠部分为五边形 .
.
方法一,作 于
于 ,
, ,
,
 ,
,
 ,
,
 .
.
方法二,由题意可得 ,
, ,
, ,
, ,
,
再计算
 ,
,

 .
.

 ,
, 当
当 时,
时, 有最大值,
有最大值, .
.
③当 时,
时, ,即
,即 与
与 重合,
重合,
设 交
交 于点
于点 ,
, 交
交 于点
于点 ,重叠部
,重叠部
分为等腰梯形 ,见图4.
,见图4.
 ,
,
综上所述:当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, .
.
 ,
,
 的最大值是
的最大值是 .
.
(1)请在图(1)中找出两对相似但不全等的三角形,并选取其中一对进行证明.
(2)求b与a的函数关系式,直接写出自变量a的取值范围.
(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).若BG=CF,求出点G的坐标,猜想线段BG、FG和CF之间的关系,并通过计算加以验证.
 查看习题详情和答案>>
查看习题详情和答案>>
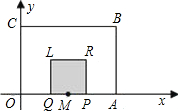 Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).(1)用含t的代数式表示点P的坐标;
(2)分别求当t=1,t=5时,线段PQ的长;
(3)求S与t之间的函数关系式;
(4)连接AC.当正方形PRLQ与△ABC的重叠部分为三角形时,直接写出t的取值范围. 查看习题详情和答案>>