摘要：小明同学是这样认为的:既然游戏对甲乙双方是公平的.所以我们可以通过对后面几次硬币正面．反面出现的情况来分配蛋糕．由原比分8∶7可知此后最多可以掷四次.最少可以掷两次赌博才可以结束．设硬币反面朝上标记“0 .乙得一分,硬币正面朝上标记“1 .甲得一分．由于先到10分游戏即可结束.所以结束游戏的可能有:000.0010.0011.0100.0101.011.1000.1001.101.11.总共10种情况．其中000.0010.0100.10004种情况乙赢, 0011.0101.011.1001.101.11.甲赢．所以甲乙双方赢得蛋糕的概率之比是6∶4．因此甲得蛋糕的.乙得蛋糕的．你认为小明的说法是否合理?说说你的理由．
网址：http://m.1010jiajiao.com/timu_id_371743[举报]
（2012•昌平区二模）类比学习：
有这样一个命题：设x、y、z都是小于1的正数，求证：x（1-y）+y（1-z）+z（1-x）＜1．
小明同学是这样证明的：如图，作边长为1的正三角形ABC，并分别在其边上截取AD=x，BE=z，CF=y，设△ADF、△CEF和△BDE的面积分别为S1、S2、S3，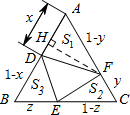
则S1=
x(1-y)sin60°，
S2=
y(1-z)sin60°，
S3=
z(1-x)sin60°．
由 S1+S2+S3＜S△ABC，得
x(1-y)sin60°+
y(1-z)sin60°+
z(1-x)sin60°＜
．
所以 x（1-y）+y（1-z）+z（1-x）＜1．
类比实践：
已知正数a、b、c、d，x、y、z、t满足a+x=b+y=c+z=d+t=k．
求证：ay+bz+ct+dx＜2k2．
查看习题详情和答案>>
有这样一个命题：设x、y、z都是小于1的正数，求证：x（1-y）+y（1-z）+z（1-x）＜1．
小明同学是这样证明的：如图，作边长为1的正三角形ABC，并分别在其边上截取AD=x，BE=z，CF=y，设△ADF、△CEF和△BDE的面积分别为S1、S2、S3，
则S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
S3=
| 1 |
| 2 |
由 S1+S2+S3＜S△ABC，得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
所以 x（1-y）+y（1-z）+z（1-x）＜1．
类比实践：
已知正数a、b、c、d，x、y、z、t满足a+x=b+y=c+z=d+t=k．
求证：ay+bz+ct+dx＜2k2．
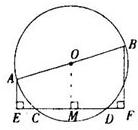16、已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD，垂足是E，BF⊥CD，垂足是F．求证：CE=DF．小明同学是这样证明的：
证明：∵OM⊥CD
∴CM=MD
∵AE∥OM∥BF
∴ME=MF
∴NE-CM=MF-MD
即CE=DF
（1）请你对小明的作业进行批改；
（2）请你给小明写出批改评语．
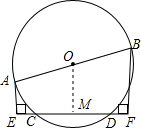已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD，垂足是E，BF⊥CD，垂足是F，求证：CE=DF，小明同学是这样证明的：证明：∵
| OM⊥CD |
| AE∥OM∥BF |
| ME=MF |
∴ME-CM=MF-MD
即CE=DF横线及问号是老师给他的，老师还写了如下评语：“你的解题思路很清晰，但证明过程欠完整，相信你再思考一下，一定能写出完整的证明过程”．请你帮助小明订正此题，好吗？ 查看习题详情和答案>>
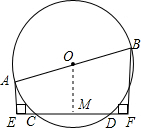已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD，垂足是E，BF⊥CD，垂足是F，求证：CE=DF，小明同学是这样证明的：
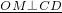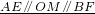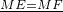
订正：∴CM=MD，∵
，∴
订正：∴CM=MD，∵
，∴
