摘要:当时.函数的图象与的图象恰好有 四个不同的交点.
网址:http://m.1010jiajiao.com/timu_id_370614[举报]
已知函数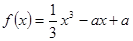
(Ⅰ)若函数 恰好有两个不同的零点,求
恰好有两个不同的零点,求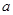 的值。
的值。
(Ⅱ)若函数 的图象与直线
的图象与直线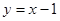 相切,求
相切,求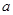 的值及相应的切点坐标。
的值及相应的切点坐标。
【解析】第一问中,利用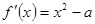
当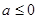 时,
时, 在
在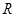 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当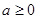 时,
时,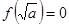 或
或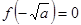 ,得
,得
第二问中,设切点为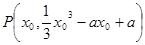 ,则
,则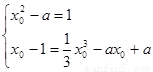
所以,当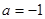 时,
时,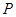 为
为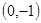 ;当
;当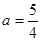 时,
时,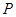 为
为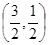
解:(Ⅰ)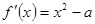 2分
2分
当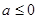 时,
时, 在
在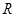 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当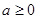 时,
时,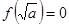 或
或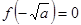 ,得
,得 4分
4分
(Ⅱ)设切点为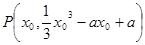 ,则
,则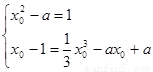 3分
3分
所以,当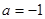 时,
时,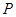 为
为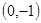 ;当
;当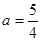 时,
时,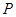 为
为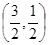
查看习题详情和答案>>
定义在[-1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[-1,1],a+b≠0时,有
>0.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若
f(x)≤m2+2am+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
查看习题详情和答案>>
| f(a)+f(b) |
| a+b |
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若
| 1 |
| 2 |
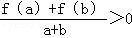 .
.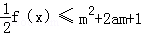 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.