摘要:象恰有四个不同交点. 即有四个不同的根.
网址:http://m.1010jiajiao.com/timu_id_370591[举报]
已知函数f(x)=ln(x2+1)-(ax-2).
(1)若|a|≤1,求f(x)的单调区间;
(2)令g(x)=
x2-ax+a+
,是否存在实数a使得f(x)的图象与g(x)的图象恰有四个不同的交点,若存在,求a的取值范围;否则,说明理由.
查看习题详情和答案>>
(1)若|a|≤1,求f(x)的单调区间;
(2)令g(x)=
| 1 |
| 2 |
| 3 |
| 2 |
已知函数f(x)=lnx,g(x)=
(a>0),设F(x)=f(x)+g(x).
(Ⅰ)求函数F(x)的单调区间;
(II)是否存在实数m,使得函数y=g(
)+m-1的图象与函数y=f(1+x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由.
查看习题详情和答案>>
| a |
| x |
(Ⅰ)求函数F(x)的单调区间;
(II)是否存在实数m,使得函数y=g(
| 2a |
| x2+1 |
已知函数f(x)=lnx,g(x)=
(a>0),设F(x)=f(x)+g(x).
(I)求函数F(x)的单调区间;
(II)若以函数y=F(x)(x∈(0,3])的图象上任意一点P(x0,y0)为切点的切线的斜率k≤
恒成立,求实数a的最小值;
(III)是否存在实数m,使得函数y=g(
)+m-1的图象与函数y=f(1+x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
| a |
| x |
(I)求函数F(x)的单调区间;
(II)若以函数y=F(x)(x∈(0,3])的图象上任意一点P(x0,y0)为切点的切线的斜率k≤
| 1 |
| 3 |
(III)是否存在实数m,使得函数y=g(
| 2a |
| x2+1 |
 ,设
,设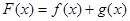
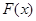 的单调区间
的单调区间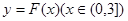 图象上任意一点
图象上任意一点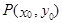 为切点的切线的斜率
为切点的切线的斜率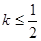 恒成立,求实数
恒成立,求实数 的最小值
的最小值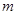 ,使得函数
,使得函数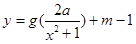 的图象与函数
的图象与函数 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数