(1)证明 //平面,——青夏教育精英家教网——

摘要：(1)证明 //平面,

网址：http://m.1010jiajiao.com/timu_id_370473[举报]

平面内n条直线，其中任何两条不平行，任何三条不共点．
（1）设这n条直线互相分割成f（n）条线段或射线，猜想f（n）的表达式并给出证明；
（2）求证：这n条直线把平面分成

+1个区域．查看习题详情和答案>>

平面直角坐标系中，O为坐标原点，已知两点M（1，-3）、N（5，1），若点C满足

（t∈R），点C的轨迹与抛物线：y²=4x交于A、B两点．
（Ⅰ）求证：

；
（Ⅱ）在x轴上是否存在一点P（m，0）（m∈R），使得过P点的直线交抛物线于D、E两点，并以该弦DE为直径的圆都过原点．若存在，请求出m的值及圆心的轨迹方程；若不存在，请说明理由．查看习题详情和答案>>

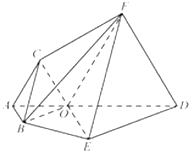平面四边形ABED中，O在线段AD上，且OA=1，OD=2，△OAB，△ODE都是正三角形．将四边形ABED沿AD翻折后，使点B落在点C位置，点E落在点F位置，且F点在平面ABED上的射影恰为线段OD的中点（即垂线段的垂足点），所得多面体ABEDFC，如图所示
（1）求棱锥F-OED的体积；
（2）证明：BC∥EF．

查看习题详情和答案>>

平面ABDE⊥平面ABC，AC⊥BC，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，AE=2BD=4，O、M分别为CE、AB的中点．
（Ⅰ）证明：OD∥平面ABC；
（Ⅱ）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由．

查看习题详情和答案>>

平面ABDE⊥平面ABC，△ABC是等腰直角三角形，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，BD=

AE=2，O、M分别为CE、AB的中点．
（I）求证：OD∥平面ABC；
（II）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由．

查看习题详情和答案>>