摘要:18.(1)解:设数列{}的公比为q.由..成等差数列.
网址:http://m.1010jiajiao.com/timu_id_370366[举报]
已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,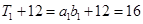 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
查看习题详情和答案>>
设等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,已知数列{bn}的公比为q(q>0),a1=b1=1,S5=45,T3=a3-b2.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求
+
+…+
.
查看习题详情和答案>>
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求
| q |
| a1a2 |
| q |
| a2a3 |
| q |
| anan+1 |
(2008•奉贤区二模)已知等比数列{an}的公比为q,Sn是{an}的前n项和.
(1)若a1=1,q>1,求
的值;
(2)若a1=1;对①q=
和②q=-
时,分别研究Sn的最值,并说明理由;
(3)若首项a1=10,设q=
,t是正整数,t满足不等式|t-63|<62,且对于任意正整数n有9<Sn<12成立,问:这样的数列{an}有几个?
查看习题详情和答案>>
(1)若a1=1,q>1,求
| lim |
| n→∞ |
| an |
| Sn |
(2)若a1=1;对①q=
| 1 |
| 2 |
| 1 |
| 2 |
(3)若首项a1=10,设q=
| 1 |
| t |