网址:http://m.1010jiajiao.com/timu_id_370111[举报]
一、选择题:
1.D 2.A 3 B 4.D 5.A 6.D 7.B 8.C 9.A 10.B 11.A 12.B
二、填空题:
三、解答题:
17.解:法(1):①∵.files/image185.gif) =(1+cosB,sinB)与
=(1+cosB,sinB)与.files/image187.gif) =(0,1)所成的角为
=(0,1)所成的角为.files/image189.gif)
②令AB=c,BC=a,AC=b
∵B=.files/image189.gif) ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac=.files/image251.gif) ,∵a,c>0。
(6分)
,∵a,c>0。
(6分)
∴(a+c)2≤48,∴a+c≤.files/image261.gif) ,∴a+b+c≤
,∴a+b+c≤.files/image261.gif) +
+.files/image191.gif) =
=.files/image264.gif) (当且仅当a=c时取等号)
(当且仅当a=c时取等号)
即2cos2B+cosB-1=0,∴cosB=.files/image272.gif) 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B=.files/image189.gif) (4分)
(4分)
(2)令AB=c,BC=a,AC=b,ΔABC的周长为.files/image275.gif) ,则
,则.files/image275.gif) =a+c+
=a+c+.files/image191.gif)
18.解法一:(1)∵PA⊥底面ABCD,BC.files/image295.gif) 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC
(2)∵AB∥CD,∠BAD=120°,∴∠ADC=60°,又AD=CD=1
∴ΔADC为等边三角形,且AC=1,取AC的中点O,则DO⊥AC,又PA⊥底面ABCD,
∴PA⊥DO,∴DO⊥平面PAC,过O作OH⊥PC,垂足为H,连DH
由三垂成定理知DH⊥PC,∴∠DHO为二面角D-PC-A的平面角
∴二面角D-PC-A的大小的正切值为2。
.files/image302.gif) (3)设点B到平面PCD的距离为d,又AB∥平面PCD
(3)设点B到平面PCD的距离为d,又AB∥平面PCD
19.解:(1)第一和第三次取球对第四次无影响,计第四次摸红球为事件A
①第二次摸红球,则第四次摸球时袋中有4红球概率为
②第二次摸白球,则第四次摸球时袋中有5红2白,摸红球概率为
∴P(A)=.files/image314.gif) ,即第四次恰好摸到红球的概率为
,即第四次恰好摸到红球的概率为.files/image316.gif) 。(6分)(注:无文字说明扣一分)
。(6分)(注:无文字说明扣一分)
(2)由题设可知ξ的所有可能取值为:ξ=0,1,2,3。P(ξ=0)=.files/image318.gif) ;
;
ξ
0
1
2
P
…………13分
(2)设C(x1,y1),D(x2,y2)设CD中点M(x0,y0),
联立直线.files/image275.gif) 与双曲线的方程得
与双曲线的方程得.files/image391.gif) ,整理得(1-3k2)x2-6kmx
,整理得(1-3k2)x2-6kmx.files/image393.gif) .
.
(2).files/image415.gif) (x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。
(x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。
(i)当m>1时,f(x)在[m,m+3]上递增。故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=.files/image423.gif) (m+3)3+
(m+3)3+.files/image272.gif) (m+3)2-2(m+3)-
(m+3)2-2(m+3)-.files/image436.gif) =
=.files/image438.gif) 得-5≤m≤1。这与条件矛盾故舍。 (6分)
得-5≤m≤1。这与条件矛盾故舍。 (6分)
(ii)当0≤m≤1时,f(x)在[m,1]上递减,在[1,m+3]上递增。
∴f(x)min=f(1),f(x)max={f(m),f(m+3)}max
又f(m+3)-f(m)=.files/image440.gif) =3(m+2)2-
=3(m+2)2-.files/image442.gif) >0(0≤m≤1),∴f(x)max=f(m+3)
>0(0≤m≤1),∴f(x)max=f(m+3)
∴|f(x1)-f(x2)| ≤f(x)max-f(x)min=f(m+3)-f(1)
≤f(4)-f(1)=.files/image232.gif) 恒成立
恒成立
故当0≤m≤1原式恒成立。 (8分)
综上:存在m且m∈[0,1]合乎题意。 (9分)
假设n=k(k≥2,k∈N*)时,ak>2。则ak+1=f(ak)>f(2)=8>2
故对于一切n(n≥2,n∈N*)均有an>2成立。 (11分)
当x∈(0,2)时.files/image455.gif) (x)<0,x∈(2,+∞)时,
(x)<0,x∈(2,+∞)时,.files/image455.gif) (x)>0,
(x)>0,
而g(2)=8-8ln2>0,即当x∈[2,+∞.files/image457.gif) 时,g(x)≥g(2)>0恒成立。
时,g(x)≥g(2)>0恒成立。
∴g(an)>0,(n≥2)也恒成立。即:an+1>8lnan(n≥2)恒成立。
而当n=1时,a2=8,而8lna1≤0,∴a2>8lna1显然成立。
综上:对一切n∈N*均有an+1>8lnan成立。
本资料由《七彩教育网》www.7caiedu.cn 提供!
.files/image236.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image253.gif)
.files/image255.gif)
.files/image257.gif)
.files/image259.gif)
.files/image268.gif)
.files/image270.gif)
.files/image278.gif)
.files/image280.gif)
.files/image282.gif)
.files/image284.gif)
.files/image286.gif)
.files/image288.gif)
.files/image290.gif)
.files/image293.gif)
.files/image297.gif)
.files/image299.gif)
.files/image301.gif)
.files/image304.gif)
.files/image306.gif)
.files/image308.gif)
.files/image310.gif)
.files/image312.gif)
.files/image320.gif)
.files/image322.gif)
.files/image324.gif)
.files/image325.gif)
.files/image327.gif)
.files/image329.gif)
.files/image331.gif)
.files/image333.gif)
.files/image335.gif)
.files/image337.gif)
.files/image339.gif)
.files/image341.gif)
.files/image343.gif)
.files/image345.gif)
.files/image347.gif)
.files/image349.gif)
.files/image351.gif)
.files/image353.gif)
.files/image355.gif)
.files/image357.gif)
.files/image359.gif)
.files/image361.gif)
.files/image363.gif)
.files/image365.gif)
.files/image204.gif)
.files/image368.gif)
.files/image370.gif)
.files/image372.gif)
.files/image374.gif)
.files/image376.gif)
.files/image378.gif)
.files/image380.gif)
.files/image382.gif)
.files/image384.gif)
.files/image386.gif)
.files/image388.gif)
.files/image395.gif)
.files/image397.gif)
.files/image399.gif)
.files/image401.gif)
.files/image403.gif)
.files/image405.gif)
.files/image407.gif)
.files/image409.gif)
.files/image411.gif)
.files/image413.gif)
.files/image417.gif)
.files/image419.gif)
.files/image421.gif)
.files/image425.gif)
.files/image427.gif)
.files/image429.gif)
.files/image431.gif)
.files/image445.gif)
.files/image447.gif)
.files/image449.gif)
.files/image451.gif)
.files/image453.gif)
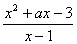 在x=1处连续,则
在x=1处连续,则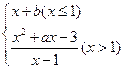 在x=1处连续,则
在x=1处连续,则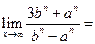 ___
___ 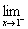 在点x=1处连续,则a的值是___________.
在点x=1处连续,则a的值是___________.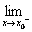 在点x=1处连续,则a的值为( )
在点x=1处连续,则a的值为( )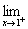 在点x=l处连续,则a等于( )
在点x=l处连续,则a等于( )