网址:http://m.1010jiajiao.com/timu_id_36623[举报]
1~10:CCBAB ADACC ; 11、 ;12、
;12、 ;13、65°;14、300π;15、①②④ð③,或 ②③④ð①; 16、94;
;13、65°;14、300π;15、①②④ð③,或 ②③④ð①; 16、94;
17、原式= ……4分 =
……4分 = …… 5分(结果为近似值亦可)
…… 5分(结果为近似值亦可)
18、x=3……4分,检验…… 5分.
19、上面是一个直四棱柱、下面是个圆锥的组合体.(2分)
 |

左视图(4分)
20、⑴(每对1格给1分,共4分)
姓名
平均成绩
中位数
众数
方差(S2)
王兰
80
80
李州
85
260
⑵李州 ……………5分
⑶对于李州,争取使学习成绩稳定下来,对于王兰,争取更好的成绩 ……………7分
(只要合理,均给分)
21、设八(2)班参加活动的有x人,则小朋友有(3x+8)人,……1分
则根据题意得: ,……3分,
,……3分,
解得9<x≤11 ……4分, ∵x是整数,∴x=10 或11.……5分
由于八(2)班参加活动的男女同学人数相等,所以只能是10人,故小朋友有38人.…7分
22、游戏对双方不公平.……1分,游戏结果分析如下:“√”表示配成紫色,“×”表示不能够配成紫色.
红
蓝
黄
红
×
√
×
蓝
√
×
×
因为P(配成紫色)= ,P(配不成紫色)=
,P(配不成紫色)= ,所以小刚得分:
,所以小刚得分: ,小明得分:
,小明得分: .所以游戏对双方不公平.……5分
.所以游戏对双方不公平.……5分
修改规则为:若配成紫色,小刚得2分,否则小明得1分,此游戏对双方才公平.(方法不唯一)……7分
23、(1) ∵∠ACB=90°,∠A=30°.
∴BC= AB.
AB.
又CD是斜边AB的中线,
∴CD=AD= AB =BD.
AB =BD.
∴BC =AD= CD =BD, ∴ 30°.
30°.
∵将△ABC沿CD折叠得△ ,
,
∴ ,
, 30°,
30°,
∴ 60°-30°=30°
60°-30°=30° ,
,
∴ ∥CB. ∴四边形
∥CB. ∴四边形 为菱形. ……5分
为菱形. ……5分
(2)∵BC=2,∴BD=2,易得 ,∴S=2
,∴S=2 .……8分
.……8分
24、(1)设垂直于墙的边长为xm,则x(12-2x)=16,解得x=2,所以垂直于墙的边长为
(2)设垂直于墙的边长为ym,则y(12-2y)=20,此方程无解,所以不能够围成.(本题也可以用二次函数说明,面积的最大值为18)……7分
25、(1)314;……3分(2)16.4;……8分(3)28.4>18,所以渔船A不会进入海洋生物保护区. ……9分
26、(1) ,顶点(1,4);……4分
,顶点(1,4);……4分
(2)Q(1,2);……5分
(3)设P( ).①当
).①当 <0时,P(
<0时,P( );②当0≤
);②当0≤ ≤3时,P(
≤3时,P( );
);
③当 >3时,P点不存在. 由①②③得点P的坐标为(
>3时,P点不存在. 由①②③得点P的坐标为( )或(
)或( )……14分
)……14分
如图,在菱形ABCD中,∠B=45°,AE是BC上的高,将△ABE沿着AE所在的直线翻折得△A![]() E.
E.
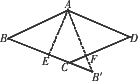
(1)请你判断△AFD的形状并说明理由.
(2)若菱形边长为2时,试求△AB′E与四边形AECD重叠部分的面积.
已知:如图,四边形ABCD为菱形,AF⊥AD交BD于点E,交BC于点F.

(1)试说明:AD2=![]() DE·DB;
DE·DB;
(2)过点E作EG⊥AF交AB于点G,若线段BE、DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为![]() .求EG的长.
.求EG的长.
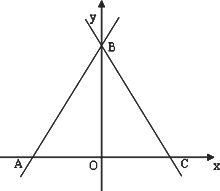
已知直线y=![]() x+4
x+4![]() 与x轴、y轴分别交于AB两点,∠ABC=60°,BC与x轴交于点C.
与x轴、y轴分别交于AB两点,∠ABC=60°,BC与x轴交于点C.

(1)试确定直线BC的解析式.
(2)若动点P从A点出发沿AC向点C运动(不与AC重合),同时动点Q从C点出发沿CBA向点A运动(不与CA重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
已知直线y=![]() x+4
x+4![]() 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
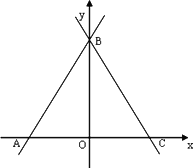
(1)试确定直线BC的解析式.
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
已知直线y=![]() x+4
x+4![]() 与x轴,y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
与x轴,y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
(1)试确定直线BC的解析式.
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.