网址:http://m.1010jiajiao.com/timu_id_36622[举报]
1~10:CCBAB ADACC ; 11、 ;12、
;12、 ;13、65°;14、300π;15、①②④ð③,或 ②③④ð①; 16、94;
;13、65°;14、300π;15、①②④ð③,或 ②③④ð①; 16、94;
17、原式= ……4分 =
……4分 = …… 5分(结果为近似值亦可)
…… 5分(结果为近似值亦可)
18、x=3……4分,检验…… 5分.
19、上面是一个直四棱柱、下面是个圆锥的组合体.(2分)
 |

左视图(4分)
20、⑴(每对1格给1分,共4分)
姓名
平均成绩
中位数
众数
方差(S2)
王兰
80
80
李州
85
260
⑵李州 ……………5分
⑶对于李州,争取使学习成绩稳定下来,对于王兰,争取更好的成绩 ……………7分
(只要合理,均给分)
21、设八(2)班参加活动的有x人,则小朋友有(3x+8)人,……1分
则根据题意得: ,……3分,
,……3分,
解得9<x≤11 ……4分, ∵x是整数,∴x=10 或11.……5分
由于八(2)班参加活动的男女同学人数相等,所以只能是10人,故小朋友有38人.…7分
22、游戏对双方不公平.……1分,游戏结果分析如下:“√”表示配成紫色,“×”表示不能够配成紫色.
红
蓝
黄
红
×
√
×
蓝
√
×
×
因为P(配成紫色)= ,P(配不成紫色)=
,P(配不成紫色)= ,所以小刚得分:
,所以小刚得分: ,小明得分:
,小明得分: .所以游戏对双方不公平.……5分
.所以游戏对双方不公平.……5分
修改规则为:若配成紫色,小刚得2分,否则小明得1分,此游戏对双方才公平.(方法不唯一)……7分
23、(1) ∵∠ACB=90°,∠A=30°.
∴BC= AB.
AB.
又CD是斜边AB的中线,
∴CD=AD= AB =BD.
AB =BD.
∴BC =AD= CD =BD, ∴ 30°.
30°.
∵将△ABC沿CD折叠得△ ,
,
∴ ,
, 30°,
30°,
∴ 60°-30°=30°
60°-30°=30° ,
,
∴ ∥CB. ∴四边形
∥CB. ∴四边形 为菱形. ……5分
为菱形. ……5分
(2)∵BC=2,∴BD=2,易得 ,∴S=2
,∴S=2 .……8分
.……8分
24、(1)设垂直于墙的边长为xm,则x(12-2x)=16,解得x=2,所以垂直于墙的边长为
(2)设垂直于墙的边长为ym,则y(12-2y)=20,此方程无解,所以不能够围成.(本题也可以用二次函数说明,面积的最大值为18)……7分
25、(1)314;……3分(2)16.4;……8分(3)28.4>18,所以渔船A不会进入海洋生物保护区. ……9分
26、(1) ,顶点(1,4);……4分
,顶点(1,4);……4分
(2)Q(1,2);……5分
(3)设P( ).①当
).①当 <0时,P(
<0时,P( );②当0≤
);②当0≤ ≤3时,P(
≤3时,P( );
);
③当 >3时,P点不存在. 由①②③得点P的坐标为(
>3时,P点不存在. 由①②③得点P的坐标为( )或(
)或( )……14分
)……14分
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
(4)试研究四边形的准等距点个数的情况.(说出相应四边形的特征及此时准等距点的个数,不必证明)
①当四边形的对角线互相垂直且任何一条对角线不平分另一条对角线或者对角线互相平分且不垂直时,准等距点的个数为
②当四边形的对角线既不垂直,又不互相平分,且有一条对角线的中垂线经过另一对角线的中点时,准等距点的个数为
③当四边形的对角线既不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点时,准等距点的个数为
④当四边形的对角线互相垂直且至少有一条对角线平分另一条对角线时,准等距点有
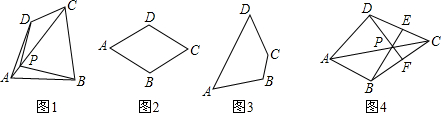
四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图1,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
(4)试研究四边形的准等距点个数的情况.(说出相应四边形的特征及此时准等距点的个数,不必证明)
①当四边形的对角线互相垂直且任何一条对角线不平分另一条对角线或者对角线互相平分且不垂直时,准等距点的个数为______个;
②当四边形的对角线既不垂直,又不互相平分,且有一条对角线的中垂线经过另一对角线的中点时,准等距点的个数为______个;
③当四边形的对角线既不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点时,准等距点的个数为______个;
④当四边形的对角线互相垂直且至少有一条对角线平分另一条对角线时,准等距点有______个(注意点P不能画在对角线的中点上).
查看习题详情和答案>>
如图1,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点。
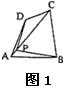

(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法);
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF,求证:点P是四边形ABCD的准等距点。
如图1,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点。


(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法);
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF,求证:点P是四边形ABCD的准等距点。
(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明)。