摘要：18．解:如图.分别过点作于点.于点．
网址：http://m.1010jiajiao.com/timu_id_358175[举报]
如图，在平面直角坐标系中，直线AB与Y轴和X轴分别交于点A、点B，与反比例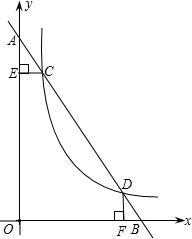
函数y=
在第一象限的图象交于点c（1，6）、点D（3，n）．过点C作CE上y轴于E，过点D作DF上x轴于F．
（1）求m，n的值；
（2）求直线AB的函数解析式；
（3）求证：△AEC≌△DFB． 查看习题详情和答案>>
函数y=| m | x |
（1）求m，n的值；
（2）求直线AB的函数解析式；
（3）求证：△AEC≌△DFB． 查看习题详情和答案>>
如图，点A是函数y=| 1 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| x |
| 2 |
| 1 |
| x |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
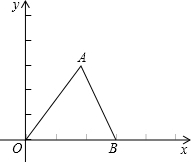如图，在平面直角坐标系中，已知：△ABC的三个顶点的坐标分别是A（4，6）、B（0，0）、C（6，0）．（1）求AO、AB所在直线的函数解析式；
（2）在△AOB内可以作一个正方形CDEF，使它的三个顶点分别落在边AO、AB上，E、F两个顶点落在OB上，请求出这个正方形四个顶眯的坐标，并在图中画出这个正方形；
（3）连接OC，在线段OC上任取一点P，过P作与x轴、y轴的不行线与OA、OB分别交于M、N两点，过M作OB边的垂线与OB交于H；你有什么发现？请写出来，并说明理由． 查看习题详情和答案>>
如图，点A是函数y=| 1 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| x |
| 2 |
| 1 |
| x |
| A、直线 | B、抛物线 |
| C、圆 | D、反比例函数的曲线 |
如图①，在边长为8
cm正方形ABCD中，E，F是对角线AC上的两个动点，它们分别从点A，点C同时出发，沿对角线以1cm/s同速度运动，过E作EH垂直AC交的直角边于H；过F作FG垂直AC交Rt△ACD的直角边于G，连接HG，EB．设HE，EF，FG，GH围成的图形面积为S1，AE，EB，BA围成的图形面积为S2（这里规定：线段的面积为0）．E到达C，F到达A停止．若E的运动时间为xs，解答下列问题：
（1）当0＜x＜8时，直接写出以E，F，G，H为顶点的四边形是什么四边形，并求x为何值时，S1=S2．
（2）①若y是S1与S2的和，求y与x之间的函数关系式．（图②为备用图）
②求y的最大值．
查看习题详情和答案>>
| 2 |
（1）当0＜x＜8时，直接写出以E，F，G，H为顶点的四边形是什么四边形，并求x为何值时，S1=S2．
（2）①若y是S1与S2的和，求y与x之间的函数关系式．（图②为备用图）
②求y的最大值．
查看习题详情和答案>>